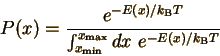The Maxwell-Boltzmann Distribution:Equilibrium Distribution of Energy
When a chemical system achieves equilibrium, it is through a process of energy transfer between the components, with energetic parts constantly giving energy away. This means that the probability distribution should favor situations where the energy is spread throughout the system and disfavor situations where any system component has a great deal of energy. The exact form of the probability distribution is an exponential function:
This equation means that the probability of finding a particle in state i or x (use i for discrete distributions and x for continuous ones) is proportional to the exponential of -E (minus the energy of the state) divided by the product of kB (Boltzmann's constant) and T (the temperature in Kelvins). What is meant by a state? Each state corresponds to a set of possible measured values. For an atom in an ideal gas, each state has particular values of the three velocity components ux, uy, and uz. States of a molecule can be indexed by the same three velocity components, plus vibrational and rotational energy levels. Since we know that any probability distribution must be normalized, we can determine the constants C and C' explicitly:
(The denominator in each case is called the "partition function".) This probability distribution describes how energy is distributed at equilibrium for an amazingly wide variety of chemical and physical systems. This probability distribution (in discrete and continuous forms) is the Maxwell-Boltzmann distribution.
Exercises Using the Maxwell-Boltzmann Distribution
The Big Picture© Andrew M. Rappe |
TheRappeGroup

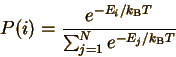 or
or