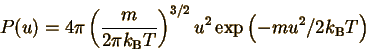The Maxwell-Boltzmann
Speed Distribution:
The Ideal
Gas
    
For many systems, including
the ideal gas, the Maxwell-Boltzmann distribution provides the probability
of finding a component in a particular state with a particular amount of
energy. In the case of the gas, many different states have the same speed;
a particle could be going left, right, up, down, back, front, or at any
angle, and still be traveling the same speed. To find the probability of
a particle having a particular speed, we must compute how many states have
the same speed, and add up the probabilities of being in any of these states.
The kinetic energy of a particle with mass m and speed u is
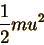
So the probability of finding
the particle in any one state is
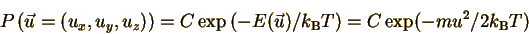
The number of states with
the same speed is given by the surface area of a spherical shell,

(This is the same factor
which enters when converting a three-dimensional Cartesian integral of
a spherically-symmetric function to spherical coordinates.) Every state
has a different velocity vector. All the states with the same speed have
velocity vectors with the same length u, pointing in different directions.
All these velocity vectors sweep out a spherical shell with radius u. Therefore,
the probability of finding an atom with a particular speed is
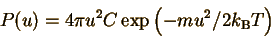 The next step is to evaluate
the normalization constant C. Since P(u) is a continuous distribution,
we must integrate over all values of u (from 0 to infinity). This involves
some advanced
mathematics, and gives (see the section on finding
average properties of the gas for a step-by-step derivation):
The next step is to evaluate
the normalization constant C. Since P(u) is a continuous distribution,
we must integrate over all values of u (from 0 to infinity). This involves
some advanced
mathematics, and gives (see the section on finding
average properties of the gas for a step-by-step derivation):
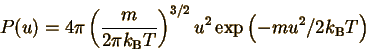
Exercises
using the Maxwell-Boltzmann Speed Distribution
-
Run the JAVA applet for 10 atoms
and a variety of temperatures. Find the most probable speed for each temperature.
How does the most probable speed change with temperature?
-
Run the applet for 2, 10, and
20 atoms at 1000K. Describe how the histogram of speeds changes as
the simulation progresses. What shape does the histogram attain after
a long run? How does the number of atoms affect the histogram?
-
Vary the number of particles
in the simulation for a fixed temperature. How does this affect the most
probable speed?
-
Which term in the Maxwell-Boltzmann
Speed distribution gives the function its shape at low speeds (near u=0)?
Which term is most important for high speeds (u>1000m/s)?
-
Thought question: Suppose
that a gas of atoms is trapped in a two-dimensional region (a box with
length and width, but just about zero height). How would the Maxwell-Boltzmann
speed distribution be different for this case?
The Big
Picture
The Maxwell-Boltzmann speed
distribution tells us the probability of finding an atom or molecule in
the gas with any particular speed. We can use this information to
make powerful statements about the gas as a whole by computing average
properties from the probability distribution.
© Andrew M. Rappe
|