The Probability Distribution:Understanding Random Systems
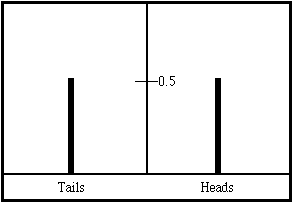
A probability distribution is a useful mathematical function for describing any situation for which the outcome is uncertain. Consider the example of coin tosses. Here, we know that the chances of getting heads or tails is 50%. Either outcome has a probability of 0.5, and the probability distribution looks like this:
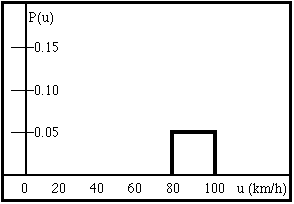
When the coin is flipped, either heads or tails must occur. Therefore, the sum of the two probabilities must add to 1 (100% total probability). Coin flips yield a discrete probability distribution, since only a finite number of outcomes are possible. Suppose that a driver varies car speeds between 80 km/h and 100 km/h, choosing all speeds in this range equally often. Since there are an infinite number of possible speeds in this range, this gives a continuous probability distribution:
The sum of the probabilities of all possible outcomes must add to 1 for any system; to reflect this, the corresponding probability distribution must be normalized:
for discrete or continuous probability distributions. Exercises Using Probability Distributions
The Big Picture© Andrew M. Rappe |
TheRappeGroup

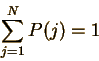 or
or