Descriptive Theory of Probability
Neglect of base rates: cab problem (Tversky and Kahneman)
A cab was involved in a hit and run accident at night. Two cab
companies, the Green and the Blue, operate in the city. You are
given the following data:
* 85% of the cabs in the city are Green and 15% are Blue.
* A witness identified the cab as Blue. The court tested
the reliability of the witness under the same circumstances that
existed on the night of the accident and concluded that the
witness correctly identified each one of the two colors 80% of
the time and failed 20% of the time.
What is the probability that the cab involved in the accident was
Blue rather than Green?
Although the two companies are roughly equal in size, 85% of
all cab accidents in the city involve Green cabs and 15% involve Blue
cabs.
Bayes's Theorem calculation
(7)
p(D | H) * p(H)
p(H | D) = ---------------------------------------------
[ p(D | H) * p(H) + p(D | not-H) * p(not-H) ]
.80 * .15 .12 .12
p(H | D) = ----------------------- = ------- = --- = .41
[.80 * .15 + .20 * .85] .12+.17 .29
Thus, p(H/D) is 12/(12+17), or .41.
Tom W.
Tom W. is of high intelligence, although lacking in true
creativity. He has a need for order and clarity, and for neat
and tidy systems in which every detail finds its appropriate
place. His writing is rather dull and mechanical, occasionally
enlivened by somewhat corny puns and by flashes of imagination of
the sci-fi type. He has a strong drive for competence. He seems
to have little feel and little sympathy for other people and does
not enjoy interacting with others. Self-centered, he nonetheless
has a deep moral sense.
Conjunction effect
Linda is 31 years old, single, outspoken and very bright. She
majored in philosophy. As a student, she was deeply concerned
with issues of discrimination and social justice, and also
participated in anti-nuclear demonstrations.
Linda is a teacher in an elementary school.
Linda works in a bookstore and takes Yoga classes.
Linda is active in the feminist movement. [F]
Linda is a psychiatric social worker.
Linda is a member of the League of Women Voters.
Linda is a bank teller. [B]
Linda is an insurance salesperson.
Linda is a bank teller and is active in the feminist movement. [B
and F].
Agnoli (1991)
In summer at the beach are there more women or more tanned women?
Gal and Baron (1996)
In one case, for example, a die was rolled
and the task was to bet which color would be on top. A subject
said, "Being the non-statistician I'd keep guessing red as there
are 4 faces red and only 2 green. Then after a number of red
came up in a row I'd figure, `it's probably time for a green,'
and would predict green."
Another subject seemed aware of the
independence of successive trials but still wanted to leave room
for an intuitive attachment to a heuristic: "Even though the
probability of Green coming up does not increase after several
Red - I always have a feeling it will. Red is the safe bet but
intuition will occasionally make me choose Green .... I know
that my intuition has nothing to do with reality, but usually they
coincide."
The hot hand
More extreme case: total neglect of probability
(Baron, Granato, Spranca, and Teubal, 1993)
Question: "Jennifer says that she heard of an
accident where a car fell into a lake and a woman was kept from
getting out in time because of wearing her seatbelt, and another
accident where a seatbelt kept someone from getting out of the
car in time when there was a fire. What do you think about
this?"
A: Well, in that case I don't think you should wear a seat
belt.
Q: How do you know when that's gonna happen?
A: Like, just hope it doesn't!
Q: So, should you or shouldn't you wear seat belts?
A: Well, tell-you-the-truth we should wear seat belts.
Q: How come?
A: Just in case of an accident. You won't get hurt as much as
you will if you didn't wear a seat belt.
Q: OK, well what about these kinds of things, when people get
trapped?
A: I don't think you should, in that case.
Another example of probability neglect
A: If you have a long trip, you wear seatbelts half way, ...
Q: Which is more likely?
A: That you'll go flyin' through the windshield ...
Q: Doesn't that mean you should wear them all the time?
A: No, it doesn't mean that.
Q: How do you know if you're gonna have one kind of accident or
the other.
A: You don't know. You just hope and pray that you don't.
Hurricanes and the 2000 election
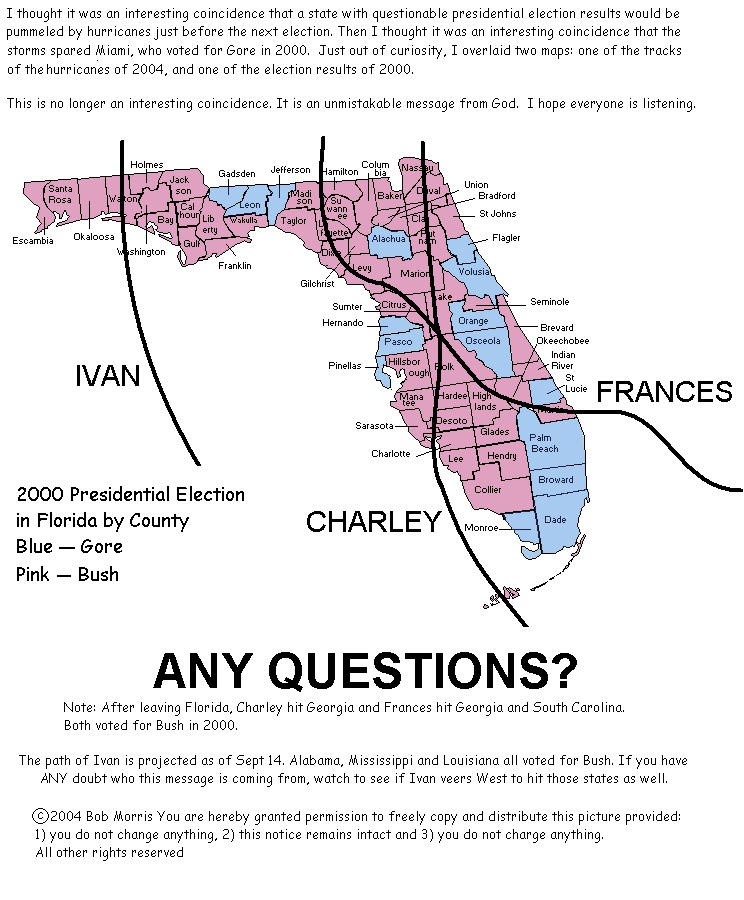
Subjective p(D|~H) is too low when the actual D is considered.
p(H) should be low, and the base rate may be ignored.
Availability effects in lethal events
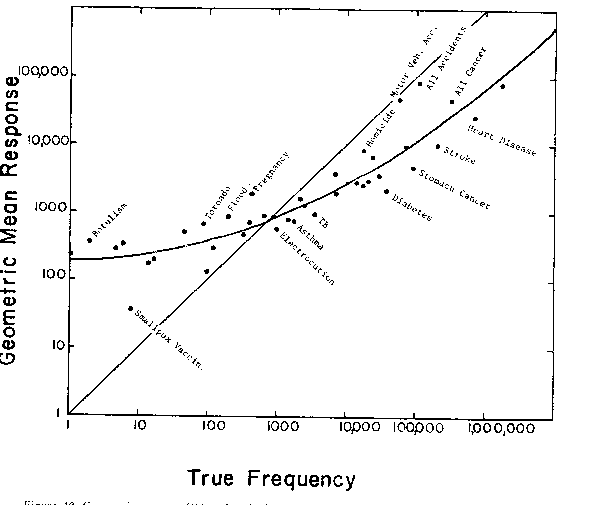
Exercises: newspaper
It is Sunday morning at 7 A.M.,
and I must decide whether to trek down to the bottom of my
driveway to get the newspaper. On the basis of past experience,
I judge that there is an 80% chance that the paper has been
delivered by now. Looking out of the living room window, I can
see exactly half of the bottom of the driveway, and the paper is
not in the half that I can see. (If the paper has been
delivered, there is an equal chance that it will fall in each
half of the driveway.) What is the probability that the paper
has been delivered? The footnote has the answer.
Answer
The prior probability is of course .80. If the paper has been
delivered, there is a .50 probability that I will not see it in the
half of the driveway that I can see. Thus, p(D|H)=.50, where D is
not seeing the paper. If the paper has not been
delivered (∼ H), p(D|∼ H)=1. So, using formula 3, the
probability of the paper’s having been delivered is
.50·.80/.50·.80 + 1·.20, or .67. If I want the
paper badly enough, I should take the chance, even though I do not see
it.
Negative mammogram
What is the probability of cancer if the mammogram is
negative, for a case in which
p(positive|cancer)=.792,
p(positive|benign)=.096, and
p(cancer)=.01? (Hint: The probability that the test is
negative is 1 minus the probability that it is positive.)
Answer
p(neg|ca)=.208,
p(neg|ben)=.904,
p(ca)=.01
| p(ca|neg) | = | | p(neg|ca)p(ca) |
|
| p(neg|ca)p(ca)
+ p(neg|ben)p(ben) |
|
| | = | | (.208)(.01) |
|
| (.208)(.01) + (.904)(.99) |
| = .0023 |
|
|
The lesson here is that negative results can be reassuring.
Aids
Suppose that 1 out of every 10,000 doctors in a certain region
is infected with the AIDS virus. A test for the virus gives a
positive result in 99% of those who are infected and in 1% of
those who are not infected. A randomly selected doctor in this
region gets a positive result. What is the probability that this
doctor is infected?
Answer
p(aids)=.0001,
p(pos|aids)=.99,
p(pos|no aids)=.01
| p(aids|pos) = | | (.99)(.0001) |
|
| (.99)(.0001) +
(.01)(.9999) |
| = .0098 |
Aids again
In a particular at-risk population, 20% are infected with
the virus. A randomly selected member of this population gets a
positive result on the same test. What is the probability that
this person is infected?
Answer
p(aids)=.20,
p(pos|aids)=.99,
p(pos|no aids)=.01
| p(aids|pos) =
| | (.99)(.20) |
|
| (.99)(.20) + (.01)(.80) |
| = .96 |
The lesson here is that tests can be useful in at-risk groups but
useless for screening (e.g., of medical personnel).
Prior conviction
You are on a jury in a murder trial. After a few days of
testimony, your probability for the defendant being guilty is
.80. Then, at the end of the trial, the prosecution presents a
new piece of evidence, just rushed in from the lab. The
defendant’s blood type is found to match that of blood found at
the scene of the crime, which could only be the blood of the
murderer. The particular blood type occurs in 5% of the
population. What should be your revised probability for the
defendant’s guilt? Would you vote to convict?
Answer
p(guilt)=.80,
p(match|guilt)=1.00,
p(match|innocent)=.05
| p(guilt|match)= | | (1.00)(.80) |
|
| (1.00)(.80) +
(.05)(.20) |
| = .988 |
Experiment
(Difficult) You do an experiment in which your hypothesis
(H1) is that females score higher than males on a test. You test
four males and four females and you find that all the females score
higher than all the males (D). The probability of this result’s
happening by chance, if the groups did not really differ (H0), is
.0016. (This is often called the level of statistical
significance.) But you want to know the probability that males
and females do differ. What else do you need (other than
more data), and how would you compute that probability?
Answer
You know
p(
D|
H0)=.0016, but you must make a judgment of the
prior
p(
H1), which is the same as 1−
p(
H0) and of
p(
D|
H1). The
latter depends on how big you judge the effect would be. Then
| p(H1|D) = | | p(D|H1)p(H1) |
|
| p(D|H1)p(H1) +
p(D|H0)p(H0) |
| . |
The difficulty of specifying the unknown quantities helps us
understand why Bayesianism is unpopular among statisticians.