The Allais Paradox
|
|
| Situation X | | |
| Option 1 | $1,000, | 1.00 |
| Option 2 | $1,000, | .89 |
| $2,000, | .10 |
| $0, | .01 |
| Situation Y | | |
| Option 3 | $1,000, | .11 |
| $0, | .89 |
| Option 4 | $2,000, | .10 |
| $0, | .90 |
|
Allais Paradox as a lottery
|
|
| Ball numbers |
| 1 | 2-11 | 12-100 |
| Situation X | | | |
| Option 1 | $1,000 | $1,000 | $1,000 |
| Option 2 | $0 | $2,000 | $1,000 |
| Situation Y | | | |
| Option 3 | $1,000 | $1,000 | $0 |
| Option 4 | $0 | $2,000 | $0 |
|
Expected utilities in the Allais Paradox
|
|
| Situation X | Option 1: | .01 u($1,000) | + .10 u($1,000) | + .89 u($1,000) |
| Option 2: | .01 u($0) | + .10 u($2,000) | + .89 u($1,000) |
| Situation Y | Option 3: | .01 u($1,000) | + .10 u($1,000) | + .89 u($0) |
| Option 4: | .01 u($0) | + .10 u($2,000) | + .89 u($0) |
|
If we follow EU and prefer option 1 to option 2 (dropping .89 u($1,000)):
.01 u($1,000) + .10 u($1,000) > .01 u($0) + .10 u($2,000)
If we prefer option 4 to option 3 (dropping u($0)):
.01 u($1,000) + .10 u($1,000) < .01 u($0) + .10 u($2,000)
Prospect Theory will explain this inconsistency.
Prospect theory: Certainty effect
($30) vs. ($45, .80)
($30, .25) vs. ($45, .20)
Two stage game: ... If you reach the second stage, you have a
choice between ($30) and ($45, .80). However, you must make this
choice before either stage of the game is played.
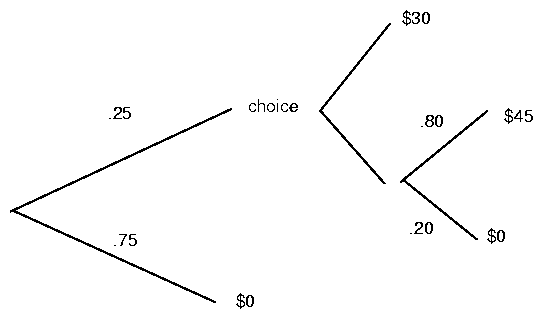
.25 u($30) < .20 u($45)
u($30) > .80 u($45)
p (pi) function
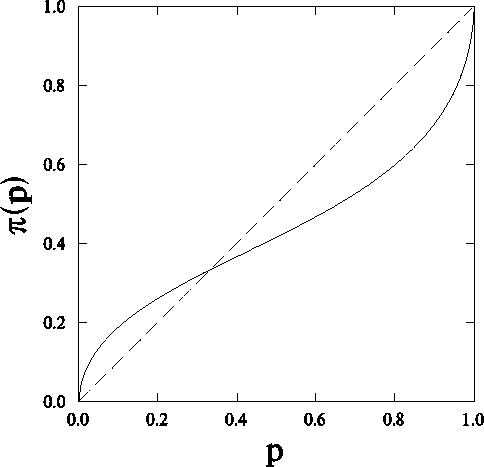
Overweighing small probabilities

($1000, .001) vs. ($1)
(-$1000, .001) vs. (-$1)
Can PT explain the Allais Paradox?
|
|
| Situation X | | |
| Option 1 | $1,000, | 1.00 |
| Option 2 | $1,000, | .89 |
| $2,000, | .10 |
| $0, | .01 |
| Situation Y | | |
| Option 3 | $1,000, | .11 |
| $0, | .89 |
| Option 4 | $2,000, | .10 |
| $0, | .90 |
|
Surcharge vs. discount: Does this make sense?
From California CIVIL CODE SECTION 1747-1748.7 :
"1748.1. (a) No retailer in any sales, service, or lease
transaction with a consumer may impose a surcharge on a cardholder who
elects to use a credit card in lieu of payment by cash, check, or
similar means. A retailer may, however, offer discounts for the
purpose of inducing payment by cash, check, or other means not
involving the use of a credit card, provided that the discount is
offered to all prospective buyers."
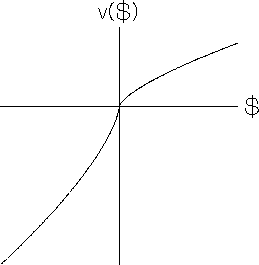
Value function
Kahneman, Knetch, & Thaler (1990)
Sellers had mug:
"Would you sell it for $0.25? for $0.50? ... for $9.25?"
Median $7.12
Buyers:
"Would you buy a mug for $0.25? for $0.50? ... for $9.25?"
Median $2.87
Choosers:
"For each amount, would you rather have that amount in cash or a mug?"
Median $3.12
Implications of status-quo (endowment) effect
Libertarian paternalism
(Choose good defaults.)
Confounded with omission bias and default bias.
Do defaults save lives? (Johnson and Goldstein, 2003)
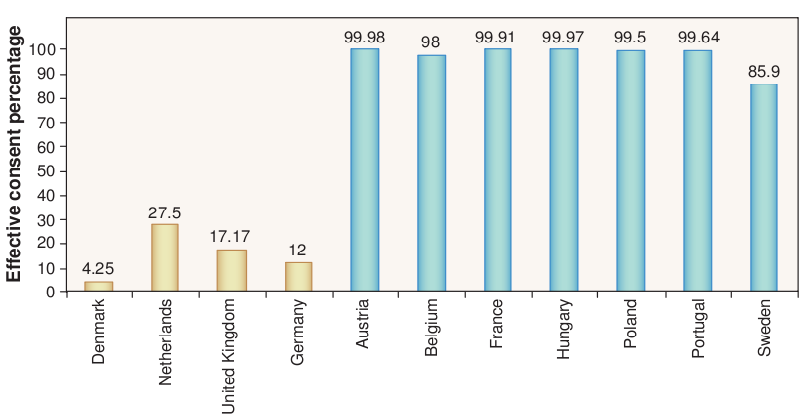
Risk aversion for gains, risk seeking for losses
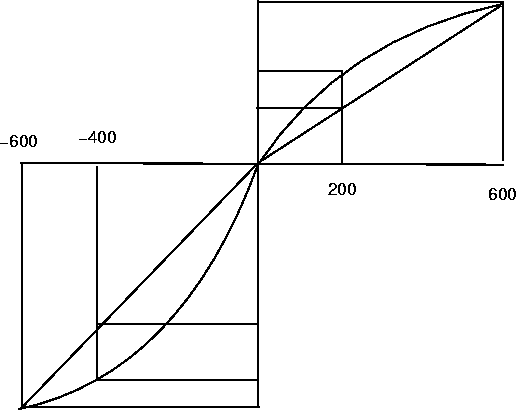
Asian disease problem

Imagine that the U.S. is preparing for the outbreak of an unusual
Asian disease, which is expected to kill 600 people. Two
alternative programs to combat the disease have been proposed.
Assume that the exact scientific estimate of the consequences of the
programs are as follows:
Program A: (200 saved)
Program B: (600 saved, .33)
Program A: (400 die)
Program B: (600 die, .67)
Framing effect
Inspector: Now, you wish to report a murder?
Depp: No, some people tried to kill me.
Inspector: I was told you were reporting a murder.
Depp: Attempted murder.
Inspector: Ah, that is not so serious.
Depp: No, not when you downgrade it from murder. When you upgrade it from room service, it’s quite serious.
From "The tourist". Johnny Depp plays the title character.
The Machina triangle
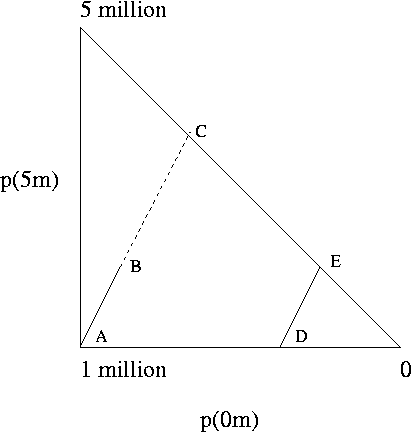
This is a general map of three-outcome gambles (Mark Machina's
idea). In the lower left corner, the subject gets the medium
outcome for sure (1 million, here). Other gambles are composed
by increasing the probability of the high outcome (5 mission),
the low outcome (0), or both. The upper left is the high outcome
for sure and the lower right is 0 for sure.
If people follows EU, indifference curves will be lines like
those drawn inside the triangle, all parallel, but possibly
different in slope from those drawn here. If the slope is
higher, people will prefer A to B and C, and they will prefer D
to E. If the slope is lower, the reverse.
The Machina triangle and Prospect Theory

One way to summarize some results of Prospect Theory is that
the slopes are higher as you move toward the upper left, a
"fanning out." This corresponds to increased risk aversion as
things get better.
Thus, people prefer A to B, but they will prefer E to D, in
Allais' paradox. This is the common consequences effect.
Notices that this is dependent on a fixed difference in
the probability of the high outcome, traded off with a fixed
difference in the probability of the low outcome.
People likewise prefer A to C even when the prefer E to
D. This is the common ratio effect, as shown in the
diagram of the certainty effect, above. Here the ratio of
the probabilities if the high and middle outcomes
are the same. In the certainty effect as presented above, the
high outcome is $45 and the middle is $30.




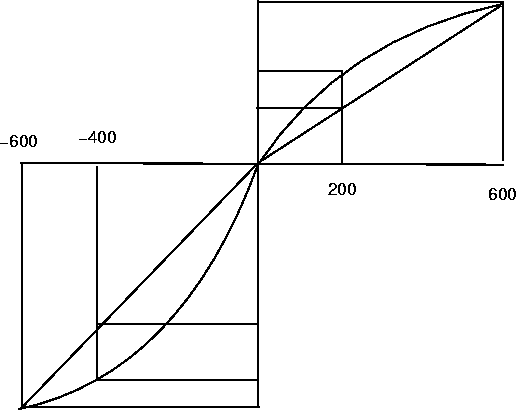
 This is a general map of three-outcome gambles (Mark Machina's
idea). In the lower left corner, the subject gets the medium
outcome for sure (1 million, here). Other gambles are composed
by increasing the probability of the high outcome (5 mission),
the low outcome (0), or both. The upper left is the high outcome
for sure and the lower right is 0 for sure.
This is a general map of three-outcome gambles (Mark Machina's
idea). In the lower left corner, the subject gets the medium
outcome for sure (1 million, here). Other gambles are composed
by increasing the probability of the high outcome (5 mission),
the low outcome (0), or both. The upper left is the high outcome
for sure and the lower right is 0 for sure.