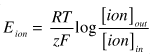
The Nernst equation expresses the balance between the electrical and chemical driving forces on an ion. It may be stated as follows:

The equilibrium potential for an is directly proportional to the log of the ratio of the extracellular over the intracellular concentrations, or

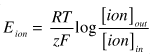
For example: the equilibrium potential for K, EK, is directly proportional to the log of the ratio of [K]out divided by [K]in. Notice that since the [K]out is usually about ten times smaller than the [K]in, the log of this ratio is near 1 and is negative. So the equilibrium potential for K will also be negative.

The exact value depends on the constants. Where concentrations are molar,

• R is the universal gas constant (8.314 J/deg-mole). We are dealing with diffusing molecules, reflecting the probability of an ion crossing the membrane.
• T is the absolute temperature (degrees Celsius + 273 = degrees Kelvin).
• z is the charge on the ion (which is 1 for potassium and sodium, 2 for calcium, and -1 for chloride).
• F, the Faraday, which is 96,500 coulombs/mole. (This constant allows us to relate voltage to ion concentration.)

But the important thing is their product, RT/zF which for a monovalent, positive ion at room temperature equals

• 25 mV if the natural logarithm of the concentration ratio has been taken
• 58 mV if the log to the base ten of the concentration ratio has been taken

Sample calculations for EK and ENa

• Calculations of EK and ENa for squid axon:
  EK   = 58 * log {20 mM/400 mM} = -75 mV
  ENa = 58 * log {440 mM/50 mM} = +55 mV

  The concentrations of K and Na in seawater and inside an squid axon, used in these calculations, are typical but may vary a bit in original papers that you may read. For example, the salinity of Woods Hole water and Plymouth, England, water is slightly different! Also, the measuements of internal concentration vary somewhat with the experimenter and certainly depend on whether the axon is damaged. Finally, remember that equilibrium potentials depend on the temperature. The calculations made here are for room temperature but Hodgkin and Huxley's experiments were done at 6.3 °C (which would change EK to -70 mV for these concentrations).

• Calculations of EK and ENa for terrestrial animals:
  EK   = 58 * log {5 mM/140 mM} = -84 mV
  ENa = 58 * log {140 mM/14 mM} = +58 mV

  The concentrations of K and Na in salines used for frog and mammalian experiments are close enough to one another to enable us to make a general, illustrative calculation. Again remember that temperature matters: although we have made the calculation at room temperature (frog experiments), mammals exist at 37.5 °C. At 37.5 °C, ENa would be +60 mV, a small difference (since T in the equation is in degrees Kelvin).