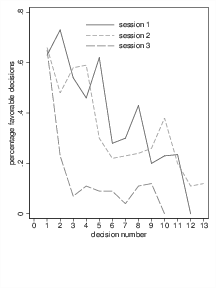
| Figure 1: Results redrawn from the graph provided in Danziger et al. (2011a). |
Judgment and Decision Making, Vol. 11, No. 6, November 2016, pp. 601-610
The irrational hungry judge effect revisited: Simulations reveal that the magnitude of the effect is overestimatedAndreas Glöckner* |
Danziger, Levav and Avnaim-Pesso (2011) analyzed legal rulings of Israeli parole boards concerning the effect of serial order in which cases are presented within ruling sessions. They found that the probability of a favorable decision drops from about 65% to almost 0% from the first ruling to the last ruling within each session and that the rate of favorable rulings returns to 65% in a session following a food break. The authors argue that these findings provide support for extraneous factors influencing judicial decisions and cautiously speculate that the effect might be driven by mental depletion. A simulation shows that the observed influence of order can be alternatively explained by a statistical artifact resulting from favorable rulings taking longer than unfavorable ones. An effect of similar magnitude would be produced by a (hypothetical) rational judge who plans ahead minimally and ends a session instead of starting cases that he or she assumes will take longer directly before the break. One methodological detail further increased the magnitude of the artifact and generates it even without assuming any foresight concerning the upcoming case. Implications for this article are discussed and the increased application of simulations to identify nonobvious rational explanations is recommended.
Keywords: decision making, legal realism, mental depletion, rationality, methods
In decisions in various contexts, individuals do not strictly adhere to standards of rationality, in that judgments and choices are influenced by many irrelevant factors such as changes in presentation format (e.g., Kahneman & Tversky, 1984), the presence of random anchors (e.g., Tversky & Kahneman, 1974), and many more. It is, however, of course socially desirable for the outcomes of legal cases to depend solely on laws and relevant facts and for influences of extraneous factors to be minimal. Decisions should, for instance, not be influenced by the order in which cases are presented or by whether the judge is exhausted or hungry.
Still, it has been demonstrated that judges show the same fallacies and biases as other individuals do (e.g., Englich, Mussweiler & Strack, 2006; Guthrie, Rachlinski & Wistrich, 2000, 2007). In psychology, the prevailing descriptive models consequently take into account that legal decision making does not follow a purely rational calculation, but involves some constructive and intuitive element, making it potentially malleable to irrelevant factors (e.g., Pennington & Hastie, 1992; Simon, 2004; Thagard, 2006).
Similarly, in the legal literature the traditional view that legal judgments can be mechanically or logically derived from official legal materials — such as statutes and reported court cases — in the vast majority of instances has been challenged by legal realism (e.g., Frank, 1930) maintaining that “legal doctrine […] is more malleable, less determinate, and less causal of judicial outcomes than the traditional view of law’s constraints supposes” (Schauer, 2013). Legal realism holds that — aside from official legal materials — extraneous factors influence legal rulings such as ideology or policy preferences of the judge, general judgment biases, and — similar to current approaches in psychology — it has been argued that rulings are partially guided by intuition (Hutcheson, 1929; see Schauer, 2013, for a review). Legal realism has a long history and many facets but it is often caricaturized by the phrase that “justice is what the judge ate for breakfast”, which also has become a trope for legal realism in general.
Figure 1: Results redrawn from the graph provided in Danziger et al. (2011a). 
In summary, there is clear evidence that judicial decision making is influenced to some degree by extraneous factors, which is also reflected in prevailing theories in law and psychology. Danziger, Levav and Avnaim-Pesso (2011a) (hereafter DLA) aim to add to this body of evidence by demonstrating that deciding multiple cases in a row influences legal outcomes of later cases. DLA analyzed 1,112 legal rulings of Israeli parole boards that cover about 40% of the parole requests of the country. They assessed the effect of the serial order in which cases are presented within a ruling session and took advantage of the fact that the ruling boards work on the cases in three sessions per day, separated by a late morning snack and a lunch break.
DLA found that the probability of a favorable decision drops from about 65% in the first ruling to almost 0% in the last ruling within each session (Figure 1). The rate of favorable rulings returns to 65% in the session following the break. DLA argue that this effect of ordering shows that judges are influenced by extraneous factors and they speculate that the effect is caused by mental depletion (Muraven & Baumeister, 2000). The argument is that, after repeated decisions, judges become exhausted, hungry or mentally depleted and use the simple and less effortful strategy to stick with the status quo by rejecting the request resulting in what could be called an “irrational hungry judge effect”.
Considering the tremendous consequences for human beings, the large magnitude of the effect, and the fact that the investigated boards decide almost half of the parole requests in Israel, these results are unexpected and potentially alarming. Consequently the article has attracted attention and the supposed order effect is considerably cited in psychology (e.g., Evans, Dillon, Goldin & Krueger, 2011), law (e.g., Schauer, 2013), economics (e.g., Kamenica, 2012), and beyond (e.g., Gibb, 2012; Yamada et al., 2012).1 The fact that — in line with the trope for legal realism mentioned above — eating (or not) is considered important for legal rulings according to DLA might have additionally contributed to the tendency to cite it heavily.
One further factor that most likely contributed to the popularity of the article is the large magnitude of the effect. A drop of favorable decisions from 65% in the first trial to 5% in the last trial as observed in DLA is equivalent to an odds ratio of 35 or a standardized mean difference of d = 1.96 (Chinn, 2000). This is more than twice the size of the conventional limit for large effects. The meta-analytic estimate for effect of mental depletion, which is considered as potential explanation for the drop, is d = –0.10 to 0.25 (publication-bias corrected), meaning that on average only small effects of mental depletion can be expected (Carter & McCullough, 2013).2 Similarly, a recent multi-lab registered replication study involving 23 labs (N= 2,142) found an effect of d = 0.04 and not significantly different from zero (Hagger & Chatzisarantis, 2016). Hence, under the assumption that mental depletion is causing the findings, the magnitude of the effect observed by DLA is surprisingly large. It might, however, be argued that manipulations of depletion and exhaustion might be stronger in reality than in the lab causing stronger effects.
Considering the latter issue and taking into account that the potential costs for giving wrong advice are high, it seems justified to take a closer look at the results and the analyses on which they are based.
One crucial assumption permitting conclusions concerning the effect of case ordering is that case ordering is random or at least not driven by hidden factors that are not taken into account in the analysis. If more severe cases went first, for example, and severe cases at the same time reduced the likelihood of favorable decisions, spurious correlations could result. In their regression analyses, DLA take this concern into account by including reasonable control variables for substantive factors that might influence both ordering and rulings. They show that the results remain robust when controlling statistically for severity of offence, previous imprisonment, months served, participation in a rehabilitation program, and proportion of previous favorable decisions.
Still in a direct reply to DLA, it has been argued that case order is influenced by systematic factors that DLA did not account for (Weinshall-Margel & Shapard, 2011). Specifically, Weinshall-Margel and Shapard (2011) conducted informal interviews with persons involved in the parole decision process (including a panel judge) and came to the conclusion that case ordering is not random. They argue, among other things, that the downward trend might be due to the fact that, within each session, unrepresented prisoners usually go last and are less likely to be granted parole than prisoners who are represented by attorneys. In a response, Danziger, Levav and Avnaim-Pesso (2011b) show that the downward trend also holds when controlling for representation by an attorney although they do not report whether the magnitude of the effect remains the same, which seems unlikely given the correlation pattern reported above. Note also the more general methodological problem that statistical control need not remove the full effect of a variable measured in rough categories (e.g., severity of offence) or with error.
A second, potentially more subtle, concern is that results might be driven by factors that systematically influence judges’ decisions to take a break. DLA analyze whether properties of a case influence the likelihood of taking a break afterwards. They report that the substantive case properties mentioned above do not predict when a break is taken. Furthermore, they argue that judges do not know details of the upcoming case such as whether the prisoner has a previous incarceration record or not. Interestingly, Weinshall-Margel and Shapard still report their interviewees to state that judges might aim to finish a set of cases (e.g., to complete all cases from one prison) within a session. This indicates that some organizational planning occurs. At first glance, however, it seems hard to understand how this mere organizational planning of when to end a session without taking into account any details of the case could contribute to the downward trend. I will discuss this issue in detail in the next section.
In summary, in their reply DLA (2011b) argue that they could rule out all alternative explanations and therefore uphold their conclusion that parole decisions are influenced by legally irrelevant factors in that repeated choice is causing a decreasing likelihood for making favorable decision as the session progresses.
If we accept that the effect of ordinal position also holds after all reasonable substantive factors that might have influenced ordering and decisions to take a break are ruled out, we must still ask whether more subtle factors could explain the observed effects, without assuming that judgments are influenced to a large degree by irrelevant factors. One major concern is the effects of selective dropouts and rational time management when to end a session in order to complete cases or sets of cases within it. Selective dropout in this context refers to the possibility that — for whatever reason — cases with favorable rulings have a lower likelihood to be in the sample of cases with higher ordinal number in a session than cases with unfavorable rulings.
DLA report that favorable rulings take longer (M = 7.37 min, SD = 5.11) than unfavorable rulings (M = 5.21 min, SD = 4.97). The number of cases completed in each session varies between 2 and 283 and DLA present rulings for 10 to 13 cases within each session, with the last ruling having a probability of zero (or in one case close to zero) to be favorable, respectively. Consequently, the number of observations within each session decreases with ordinal position and the last observations in a session are likely to consist of a few observations only. Considering that favorable rulings take longer than unfavorable rulings, the dropout is not random. On average, sessions that consist of mainly unfavorable decisions will allow judges to make many rulings. Therefore, in the reduced sample of observations constituting the data for higher ordinal positions, the relative frequency of rulings from sessions with mainly unfavorable decisions increases.4
Judges have to finish cases before they take a break. To avoid starving, they are likely to avoid starting potentially complex cases (or sets of cases) directly before the break. It seems reasonable to assume that simple surface features that are available before investigating the case in detail (e.g., amount of material, kind of the request, representation by an attorney, some specifics of the attorney, the prison, or the prisoner) allow judges roughly to estimate the time the next case will take above chance level. Importantly, such surface features could also be unrelated to the content features that could produce non-random ordering of cases and that DLA already control for in their analysis.
Still, as mentioned above, it is hard to see whether and to what degree not starting overly long cases before a break would lead to the observation of downward sloping effects without assuming that judgments are influenced by extraneous factors at all. I conducted simulations to make the effect visible.
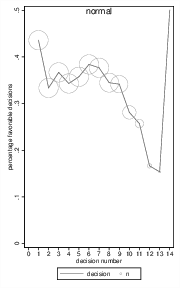
Figure 2: Simulated favorability ratings of a perfectly rational judge who works on cases with the speed observed by DLA and starts a new session for each case that would go over the time limit. The left chart depicts a distribution assuming that decision times follow a Weibull distribution, while the right chart shows results assuming a normal distribution. Circle diameter indicates the sample size for each observation and shows the large degree of dropouts within sessions. 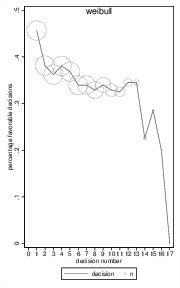
I simulated the rulings of an ideal judge who makes choices without errors and biases. I assume that she has a rough time limit for each session and works on cases until recognizing that a case would go over this limit. The case that would be too long would not be solved any more in the current session, but it would be the first case in the next session.5
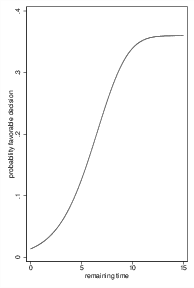
Figure 3: Distribution of decision times (left) and effect of the remaining time on the proportion of favorable cases in the remaining selective sample (right). 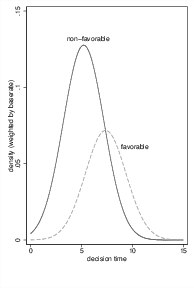
The results indicate that, following the approach by DLA, a rational judge working on cases that are presented in random order would show a strongly decreasing probability of a favorable decision towards the end of the session. Even the shape of the curve and the magnitude of the effect are comparable to that observed by DLA. Simulations assuming normally distributed decision times (Figure 2, right) or more realistic positively-skewed decision times that follow a Weibull distribution (Figure 2, left) lead to similar conclusions, and repeated simulations show that the qualitative pattern of results is robust to changes in distributional assumptions. As one could expect, however, estimations become unstable for higher decision numbers due to the low number of remaining observations (see Figure 2, size of circles), resulting in occasional peaks to high or zero percentages. Not surprisingly, statistical analysis reveals that the downward trend is significant and that first decisions are more favorable than later ones, as it was found by DLA.
Figure 3 shows why this effect appears for the normally distributed case. Distributions of decision time have different means with favorable cases taking longer than unfavorable ones (left panel). Consequently, the relative frequency of favorable cases (in all cases) that would still fit in the session decreases with remaining time. In our example, if 15 minutes remain in the session, essentially all cases would still be started since such long times are rare both for favorable and unfavorable cases (Figure 3, left). The ratio of favorable and unfavorable cases therefore roughly reflects the overall ratio in the population. For 5 minutes remaining, however, only 12% of the favorable cases could still be included in the session, whereas the respective proportion for unfavorable cases is much higher at 46%. Hence, the relative frequency of favorable cases, as compared to all cases, decreases with the time that remains causing selective dropout.
The cumulative probability distribution for favorable decisions (taking into account differences in base rates for both events) is plotted in the right panel of Figure 3. For long remaining times, the proportion of favorable cases is close to the base rate of 36%. For short remaining times, the proportion approaches values close to zero. With an increasing decision number within a session, the remaining time decreases, causing the downward sloping effect. Since sessions can stop after 1 to 14 decisions, the stopping effect is not only found after case 14, but already to a smaller degree for earlier cases. Hence, the probability can be expected to drop from 36% to zero percent for later rulings.
It remains to be explained why the proportion of favorable rulings (in both the simulation and the DLA data) peaks beyond 36% in the first round. This “beginning effect” is indirectly caused by the above mechanism as well, since the session is more likely to end before a favorable ruling than before an unfavorable ruling. The probability mass that is missing in the last decision of the previous session adds to the probability mass of favorable cases in the first decision of the next session (either on the same day or the first session of the next day). If one assumes that planning is not only done for single cases, but also occasionally concerns sets of cases (Weinshall-Margel & Shapard, 2011), this would explain why the probability of a favorable decision in the second and third ruling in a session is also above the base rate of 36%.6 Furthermore, the observation by DLA that the overall length of sessions varies considerably does not speak against the planning explanation since the effect also holds under the assumption that judges have implicit time limits that vary from session to session. Also, it should be noted that the planning described here is merely organizational and does not require any foresight concerning how the case will be decided. All it requires is that the judges have a rough estimate, whether the next case will be quick or take longer.
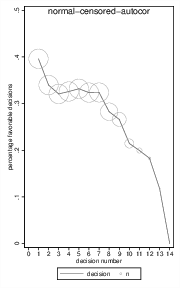
Figure 4: Simulated favorability ratings including the effects of censoring the last 5% of cases within each session (left) and additional autocorrelation (right). Circle diameter represents n. 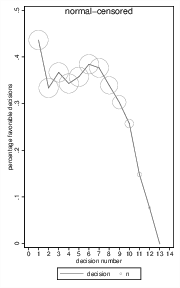
After demonstrating that rational time management and selective dropout can cause dramatic drops in favorability ratings, the robustness of this finding and the influence of further factors should be investigated. Two factors are considered. First, DLA report that they censor their data, in that the last 5% of the cases in each session are dropped, with the intention of eliminating small samples at higher ordinal positions. Second, as mentioned above (Footnote 4) results from DLA indicate that there is an autocorrelation in the time-series, in that rulings correlate with previous ones. Since the consequences of these factors are again hard to anticipate, I conducted further analyses to explore their effects.
To investigate the effect of censoring, I dropped the last 5% of the rulings within each session in the normal distribution data-set from above (Figure 2, right) and analyzed the data again. Results remained largely the same, but censoring increased the magnitude of the drop (Figure 4, left), which was also observed for the Weibull data set and was consistently replicated in further simulations. Hence, censoring artificially increases selective dropout, and therefore it should not be used when analyzing the effect of ordinal position on favorability rulings.
To investigate the effect of autocorrelation, I generated new data sets (N = 50,000) based on normally distributed response times with the same parameters as above in which, however, rulings correlated with rulings directly before at a low degrees. Figure 4 (right) shows results from a data set with a (first-order) autocorrelation of r = .10 and including censoring as above. Results are generally comparable to the results from the independent data-set, and autocorrelation did not noticeably change the magnitude of the artifact.
Figure 5: Simulated favorability ratings without foresight concerning the upcoming case but including the effects of censoring the last 5% of cases within each session and autocorrelation r = .10 (N = 50,000). Circle diameter represents n. 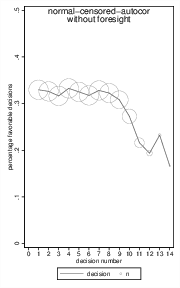
One assumption underlying the simulations reported so far is that judges plan ahead and do not start a case that would be too long to finish within the time limit for a session. This planning would require some degree of foresight in that judges (or other people administratively involved) generate estimates of the time required for finishing the upcoming case. Thereby estimates do not need to be exact to generate the artifact and can be based on rough surface cues as mentioned above as well. Also cues for time management might be (consciously or unconsciously) conveyed by administrative persons involved in the process of handling cases (Pfungst, 1911). As mentioned above, DLA state that details about the upcoming case are not known to the members of the board in advance. Since, however, DLA did not have full control over the situations, the existence of such cues cannot be entirely ruled out.
Still, presuming foresight in many cases is admittedly a relatively strong assumption. I therefore tested whether the analysis conducted by DLA would also generate similar artifacts without foresight in that judges stop after a case went over the available time limit.7 When conducting this analysis without censoring and autocorrelation, all artifacts disappear, as one would expect. Interestingly, however, when including censoring and autocorrelation a downward sloping effect appears again (Figure 5). The reason for this is that cases with favorable rulings are more likely to hit the time limit than cases with unfavorable ruling due to the mere fact that they are longer. Dropping 5% of the cases at the end means often postponing this last case, which is more likely favorable than unfavorable. Hence, censoring causes selective dropout of favorable cases even without foresight and artificially induces a downward sloping effect of favorable ruling. The effect was, however, smaller than in the simulations with foresight and caused a drop of roughly 15% only.
In a comprehensive analysis of legal rulings of Israeli parole boards DLA identified that the proportion of favorable rulings decreases with serial order within a session but goes back to the initial level after a session break that includes eating a meal. This finding is important as well as potentially alarming, since both serial order and food supply are clearly extraneous factors that should not affect whether a parole request is decided favorable or not. DLA argue that their findings indicate that extraneous variables influence judicial decisions and cautiously interpret their finding with reference to a mental depletion account.
I critically revisited this interpretation and tested whether the core of the conclusion — namely that order and mental depletion causally influence the outcome of legal judgments — can be made on the basis of the presented data. Specifically, I tested whether the observed downward trend could also results from selective dropout of favorable cases due to rational time management, censoring of data and autocorrelation. The analysis shows that large parts — but admittedly not all aspects, see below — of the findings could be accounted for by this explanation.
The simulations show that the seemingly dramatic drop of favorable rulings from 65% to almost 0% towards the end of each session does not conclusively indicate bias or error in judicial decision making. A drop of comparable — although somewhat smaller — magnitude would be produced by a (hypothetical) rational judge who aims to avoid starting work on cases that could not be completed in the time that remains in the current session. Furthermore, the simulations revealed that the practice of censoring data within a session is problematic and artificially induces a downward sloping effect even without foresight and under the less restrictive assumption that judges stop each session after a time limit has been passed. Hence, the analyses by DLA do not provide conclusive evidence for the hypothesis that extraneous factors influence legal rulings.
It has to be acknowledged that the analyses reported in this paper do not preclude that serial order and mental depletion might have affected the legal judgments analyzed by DLA. The analysis, however, demonstrates that there is a possible alternative explanation for large parts of the results within a rational framework that does not require the assumption of any influence of extraneous factors. The strong downward-sloping effect could — at least in parts — simply reflect a statistical artifacts.
Still, rational time management and selective dropout cannot account for all aspects of the data by DLA. First, the magnitude of the effects reported in the simulations was somewhat smaller than the magnitude of the original effects.8 This was mainly due to the fact that, second, in the original data the percentage of favorable rulings started at a higher level than in the current simulations (i.e. 65% instead of 45%). Particularly, the high starting rates at the beginning of the day (and not only after the breaks) are hard to explain by my account since postponing cases to a different day and panel seems not overly likely.9 Third, since the statistical effects described here are driven by ordinal position, they cannot easily explain the effects of time on favorable rulings reported in DLA as well. Fourth, the shape of the curves differ in some details in that the empirical curve tended to be smoother whereas the simulated data showed stronger drops at the beginning and the end a flatter area in between. Finally, given that according to DLA the setting might have precluded direct foresight concerning the upcoming case to some degree, the remaining effects of rational time management could be estimated to account for a drop of 15% to 45% only.
In sum, rational time management and selective dropout — although potentially being important — can explain the findings by DLA only in parts. Hence, further factors may exist that contributed to the observed downward-sloping effect. The remaining differences could potentially be explained by other methodological factors such as the issue of non-random ordering in that prisoners represented by attorneys went first (Weinshall-Margel & Shapard, 2011). Alternatively, extraneous factors such as causal effects of serial case ordering and mental depletion might have played a role. Since the data are not available10 for further detailed analyses and the exact circumstances under which the rulings were made cannot be fully reconstructed, these issues have to be addressed in further studies.
The analyses reported here indicates that the effect of serial order and mental depletion is overestimated in the original work by DLA. Rational time management concerning when to take a break and effects of non-random ordering of cases with represented prisoners going first identified by Weinshall-Margel and Shapard (2011) are lumped together with potential effects of serial order and mental depletion so that the latter are overestimated. Disentangling these influences should lead to more reasonable (smaller) estimates concerning the magnitude of the effect. According to previous findings on mental depletion, the “irrational hungry judge effect” should at best be small in magnitude (if existing at all; see Carter & McCullough, 2013), which might render the observed extraneous influence less relevant from a practical point of view and the need for state interventions less urgent.
More generally, the analysis shows that sometimes there is a nonobvious rational basis for irrational-looking behavior. Computer simulations as well as formal mathematical analyses are measures to identify them. Such analyses have revealed, for example, that whole strands of literature supposedly demonstrating irrational behavior such as spreading apart effects after choice (Chen & Risen, 2010), unrealistic optimism (Harris & Hahn, 2011) or the adaptive usage of simple heuristics (Jekel & Glöckner, in press) are methodological or statistical artifacts that would be shown by completely rational agents as well. I argue that simulations of rational agents and formal mathematical analyses should be used earlier and more intensely in the research process to investigate findings of supposedly hugely irrational behavior before jumping to the conclusion that legal actors — or any other individuals — are irrational.
Carter, E. C., & McCullough, M. E. (2013). Is ego depletion too incredible? Evidence for the overestimation of the depletion effect. Behavioral and Brain Sciences, 36(06), 683–684. http://dx.doi.org/10.1017/S0140525X13000952.
Chen, M. K., & Risen, J. L. (2010). How choice affects and reflects preferences: revisiting the free-choice paradigm. Journal of Personality and Social Psychology, 99(4), 573–594.
Chinn, S. (2000). A simple method for converting an odds ratio to effect size for use in meta-analysis. Statistics in Medicine, 19(22), 3127–3131.
Danziger, S., Levav, J., & Avnaim-Pesso, L. (2011a). Extraneous factors in judicial decisions. Proceedings of the National Academy of Sciences, 108(17), 6889–6892. http://dx.doi.org/10.1073/pnas.1018033108.
Danziger, S., Levav, J., & Avnaim-Pesso, L. (2011b). Reply to Weinshall-Margel and Shapard: Extraneous factors in judicial decisions persist. Proceedings of the National Academy of Sciences of the United States of America, 108(42), E834-E834. http://dx.doi.org/10.1073/pnas.1112190108.
Englich, B., Mussweiler, T., & Strack, F. (2006). Playing dice with criminal sentences: The influence of irrelevant anchors on experts judicial decision making. Personality and Social Psychology Bulletin, 32(2), 188–200.
Evans, A. M., Dillon, K. D., Goldin, G., & Krueger, J. I. (2011). Trust and self-control: The moderating role of the default. Judgment and Decision Making, 6(7), 697–705.
Frank, J. (1930). Law and the modern mind. New York: Brentano’s.
Gibb, B. C. (2012). Judicial chemistry. Nature Chemistry, 4(1), 1–2. http://dx.doi.org/10.1038/nchem.1229.
Guthrie, C., Rachlinski, J. J., & Wistrich, A. J. (2000). Inside the judicial mind. Cornell Law Review, 86, 777–830.
Guthrie, C., Rachlinski, J. J., & Wistrich, A. J. (2007). Blinking on the bench: How judges decide cases. Cornell Law Review, 93(1), 1–44.
Hagger, M. S., & Chatzisarantis, N. L. D. (2016). A Multilab Preregistered Replication of the Ego-Depletion Effect. Perspectives on Psychological Science, 11(4), 546–573. http://dx.doi.org/10.1177/1745691616652873.
Hagger, M. S., Wood, C., Stiff, C., & Chatzisarantis, N. L. (2010). Ego depletion and the strength model of self-control: a meta-analysis. Psychological Bulletin, 136(4), 495–525.
Harris, A. J., & Hahn, U. (2011). Unrealistic optimism about future life events: a cautionary note. Psychological Review, 118(1), 135–154.
Hutcheson, J. C. (1929). The judgment intuitive: the function of the “hunch” in judicial decision making. Cornell Law Quarterly, 14, 274–288.
Jekel, M., & Glöckner, A. (in press). How to identify strategy use and adaptive strategy selection: the crucial role of chance correction in Weighted Compensatory Strategies. Journal of Behavioral Decision Making.
Kahneman, D., & Tversky, A. (1984). Choices, values, and frames. American Psychologist, 39(4), 341–350.
Kamenica, E. (2012). Behavioral economics and psychology of incentives. Annual Review of Economics, 4(1), 427–452.
Muraven, M., & Baumeister, R. F. (2000). Self-regulation and depletion of limited resources: Does self-control resemble a muscle? Psychological Bulletin, 126(2), 247–259.
Open Science Collaboration. (2015). Estimating the reproducibility of psychological science. Science, 349(6251), aac4716.
Pennington, N., & Hastie, R. (1992). Explaining the evidence: Tests of the Story Model for juror decision making. Journal of Personality and Social Psychology, 62(2), 189–206.
Pfungst, O. (1911). Clever Hans (the horse of Mr. Von Osten): a contribution to experimental animal and human psychology. New York: Holt, Rinehart and Winston (Originally published in German, 1907).
Rouder, J. N., Lu, J., Speckman, P., Sun, D. H., & Jiang, Y. (2005). A hierarchical model for estimating response time distributions. Psychonomic Bulletin & Review, 12(2), 195–223.
Schauer, F. (2013). Legal Realism Untamed. Texas Law Review, 91(4), 749–780.
Simon, D. (2004). A third view of the black box: cognitive coherence in legal decision making. University of Chicago Law Review, 71, 511–586.
Thagard, P. (2006). Evaluating Explanations in Law, Science, and Everyday Life. Current Directions in Psychological Science, 15(3), 141–145.
Tversky, A., & Kahneman, D. (1974). Judgment under uncertainty: Heuristics and biases. Science, 185(4157), 1124–1131.
Weinshall-Margel, K., & Shapard, J. (2011). Overlooked factors in the analysis of parole decisions. Proceedings of the National Academy of Sciences of the United States of America, 108(42), E833–E833. http://dx.doi.org/DOI 10.1073/pnas.1110910108.
Yamada, M., Camerer, C. F., Fujie, S., Kato, M., Matsuda, T., Takano, H., …Takahashi, H. (2012). Neural circuits in the brain that are activated when mitigating criminal sentences. Nature Communications, 3. http://dx.doi.org/10.1038/ncomms1757.
clear
set obs 10000
gen favorable = 0
replace favorable = 1 if runiform() > .64
tab favorable
gen time = .
replace time = 5.21 + rnormal()*2 if favorable == 0
replace time = 7.37 + rnormal()*2 if favorable == 1
hist time
hist time , by(favorable)
mean time, over(favorable)
gen time_count = .
replace time_count = time if _n == 1
gen session = .
replace session = 1 if _n == 1
gen decision = .
replace decision = 1 if _n == 1
forvalues x = 2/10000 {
replace time_count = time_count[_n-1] + time[_n] if _n == `x' & (time_count[_n-1] + time[_n] < 60)
replace session = session[_n-1] if _n == `x' & (time_count[_n-1] + time[_n] < 60)
replace decision = decision[_n-1] + 1 if _n == `x' & (time_count[_n-1] + time[_n] < 60)
replace time_count = time[_n] if _n == `x' & (time_count[_n-1] + time[_n] >= 60)
replace session = session[_n-1] + 1 if _n == `x' & (time_count[_n-1] + time[_n] >= 60)
replace decision = 1 if _n == `x' & (time_count[_n-1] + time[_n] >= 60)
}
bysort session: egen maxim = max(decision)
hist maxim
lgraph favorable decision
logit favorable i.decision
logit favorable decision
preserve
collapse favorable (semean) se = favorable (count) participation = favorable , by(decision)
gen ul = favorable + 1.96 * se
gen ll = favorable - 1.96 * se
twoway (line favorable decision) ///
(scatter favorable decision [aweight= participation], symbol(oh) mlwidth(vvthin)), ///
scheme(s1mono) xtitle(decision number) ytitle(percentage favorable decisions) ///
legend( lab(1 "decision") lab(2 "n") cols(3)) xlabel(0(1)14) xsize(2.5) ///
ylabel(0(0.1)0.5) yscale(r(0(0.1)0.5))
graph save Normal, replace
restore
Acknowledgment: I thank Mark Schweizer, Marc Jekel, Susann Fiedler, and Christoph Engel for helpful comments on earlier versions of this manuscript and Brian Cooper for proof reading.
Copyright: © 2016. The authors license this article under the terms of the Creative Commons Attribution 3.0 License.
This document was translated from LATEX by HEVEA.