Judgment and Decision Making, vol. 3,
no. 5, June 2008, pp. 411-416.
How to make a risk seem riskier: The ratio bias versus construal level
theoryCarissa Bonner and Ben R. Newell*
School of Psychology
University of New South Wales |
Which statement conveys greater risk: “100 people die from cancer
every day” or “36,500 people die from cancer every year”? In
statistics where both frequencies and temporal information are used
to convey risk, two theories predict opposite answers to this
question.
Construal level theory predicts that “100 people die from cancer
every day” will be judged as more risky, while the ratio bias
predicts that the equivalent “36,500 people die from cancer every
year” will result in higher risk judgments. An experiment
investigated which format produces higher risk ratings, and whether
ratings are influenced by increasing the salience of the numerical
or temporal part of the statistic. Forty-eight participants were
randomly assigned to a numerical, temporal or control salience
condition, and rated risk framed as number of deaths per day or per
year. The year format was found to result in higher perceived risk,
indicating that the ratio bias effect is dominant, but there was no
effect of salience.
Keywords: risk perception, ratio bias, construal level theory, health
statistics, framing.
1 Introduction
The perception of risk is an important area of research not only for
understanding cognitive processes, but also for its practical
applications in conveying risk information to the public. In the health
domain, perceived risk is generally regarded as the first step in
models of health behaviour, and a necessary (but not sufficient)
condition for behaviour change (see Weinstein (1993) and Van der Pligt
(1996) for reviews). Although other factors have been shown to mediate
this relationship (e.g., conscientiousness and gender; Hampson, Andrews,
Barckley, Lichtenstein & Lee, 2000), conveying a sense of risk is a
major focus of health communication, with the aim of influencing
individual judgment and decision making. The present research
investigates how risk perception is affected by the framing (cf.
Tversky & Kahneman, 1981) of incidence rates, which are often used to
convey risk information to the public.
1.1 Temporal construal
Construal Level Theory (CLT) proposes that temporal distance determines
how future events are mentally represented (Trope & Liberman, 2003).
Near events are represented at a lower level construal, defined as
concrete, specific and detailed. Distant events are represented at a
higher level construal, which are more abstract, decontexualised and
general. For example, moving house next week is likely to be described
in terms of concrete, specific actions such as packing boxes, while
next year would be described in more abstract, global terms such as a
new phase of life.
Chandron and Menon (2004) extended this theory to risk perception,
looking at the effects of message cues on judgments of health risk.
They framed risks associated with mononucleosis as occurring “every
day” or “every year”, and found that the day frame increased risk
ratings. According to CLT, the risk is represented at the same
construal level as the time frame. Since the day frame is perceived as
more concrete and proximal than the year frame, the risk seems more
immediate and threatening, resulting in higher perceived risk.
1.2 Ratio bias
The ratio bias is the tendency for people to judge a low probability
event as more likely when presented as a large-numbered ratio, such as 20/100,
than as a smaller-numbered but equivalent ratio, such as 2/10. This effect is
attributed to a tendency to focus on the frequency of the numerator
instead of the overall proportion (Kirkpatrick & Epstein, 1992).
The ratio bias has been investigated in the health domain by Yamagishi
(1997) and Pinto-Prades, Martinez-Perez and Abellán-Perpiñán
(2006). Yamagishi (1997) gave participants mortality rates of
well-known causes of death, varying both the percentage incidence rate
and population frame (deaths per 100 or 10,000 people) within subjects.
Results showed that ratings of risk were consistently higher with a
frame of 10,000 than a frame of 100, regardless of the actual
percentage incidence rate. For example, participants rated cancer as
riskier when it was described as killing 1,286 out of 10,000 people
than as killing 24.14 out of 100 people. The fact that 12.86% could be
considered more risky than 24.14% is a clear demonstration that the
ratio bias can strongly influence perception of risk. Similarly,
Pinto-Prades et al. (2006) investigated the ratio bias in terms of
choices between medical treatments with a given probability of death.
They found that the frame determined the point at which participants
reached indifference between choices: those given a smaller frame (per
100 people) would choose a particular treatment option up to a 37.1%
chance of death, while those given a larger frame (per 1000 people),
where the absolute number of deaths was higher, would only accept up to
a 17.6% chance of death for the same treatment option.
1.3 Concrete versus abstract processing
What ties the temporal construal and ratio biases together is the
difference between concrete and abstract information processing. The
more concrete the information is, the easier it is to imagine and
associate with affect (Newell, Mitchell, & Hayes, in press; Slovic,
Monahan & MacGregor, 2000), resulting in higher perceived risk. In
temporal information, using a closer temporal frame such as “every
day” increases the concreteness and proximity of the threat, and
therefore increases perceived risk (Chandron & Menon, 2004). In
numerical information, frequencies are more concrete than
probabilities or percentages (e.g., Gigerenzer & Hoffrage, 1995;
Slovic et al., 2000). For example, Newell et al. (in press) found
that frequency information led to higher ratings of the imaginability
of rare events, such as suffering the side effects of a vaccine, than
did probability information. In addition, small numbers are perceived
as being more concrete than large numbers (Denes-Raj & Epstein,
1994), leading to a bias towards the numerator of a numerical ratio.
In statistics where both frequencies and temporal information are used
to convey risk, these two biases towards concrete information will be
in opposition to each other. Construal level theory predicts that
“100 people die from cancer every day” will be perceived as more
risky due to the use of closer temporal proximity. In contrast, the
ratio bias effect predicts that “36,500 people die from cancer every
year” will result in higher risk ratings, because risk will be
inferred from the absolute number of deaths without sufficient regard
for the temporal frame (day or year). The aim of the experiment was to
investigate whether one of these effects is more dominant in health
statistics, when the biases are in opposition.
2 Method
2.1 Participants
Forty-eight undergraduate students (35 female and 13 male) from the
University of New South Wales participated for course credit, with an
average age of 19.27 years (SD = 2.43).
2.2 Design
The experiment was set up as a 3 x (2 x 11) factorial design. The
salience factor (emphasising the numerical or temporal information,
versus a control condition) was between subjects, with 16 participants
randomly assigned to each group. The format factor (every day versus
every year) and cause of death (11 causes) were repeated within
subjects, with the two formats completed one week apart. That is, each
participant filled in a first questionnaire with one format (e.g.,
year) and then returned one week later (range: 6–9 days) to fill in a
second questionnaire with the other format (e.g., day). The order of
day and year formats was counterbalanced. A similar repeated measures
design was used effectively in Yamagishi’s (1997) study, and ensures
that individual interpretations of “risk” and response tendencies
are taken into account.
2.3 Materials
Following the method of Yamagishi (1997), eleven major causes of death
were used: heart failure, stroke, pneumonia, AIDS, motor vehicle
accidents, cancer, homicide, respiratory diseases, renal failure,
heart disease, and diabetes. Mortality rates were based on the
government report Causes of Death, Australia 2003 (Australian
Bureau of Statistics, 2004). The mortality rates were approximately
equivalent for day and year formats, but were adjusted slightly to
give numbers to the nearest 100 in some cases (this was not
systematic, i.e., some rounded down and some rounded up). For example,
the diabetes statistics used were 8 per day and 2,900 per year, even
though 2,920 is the exact equivalent (i.e., 8 x 365). This approach
was taken because the generic term “every year” was used, and the
exact number of deaths from a particular cause varies each year.
The information about each cause of death was given in a single sentence
followed by a rating scale, with all eleven causes on the same page.
The order was arranged so that causes with similar incidence rates were
not consecutive. To produce the numerical or temporal salience, the
relevant information was placed at the beginning of the sentence in
bold underlined font (as shown in Table 1). The effect of the font was enhanced
by repetition for the eleven causes of death.
| Table 1: Example of salience conditions (cancer deaths per day) |
| Condition | Format |
| Control | In Australia 100 people die every day from cancer |
| Numerical | 100 people in Australia die every day from cancer |
| Temporal | Every day in Australia 100 people die from cancer |
This is similar to the method of Chandron and Menon (2004), who also
used repetition of “every day” or “every year” at the beginning of
sentences. Perceived risk was measured by a 26 point Likert scale,
anchored at 0 “no risk at all” and 25 “highest possible risk”.
This maintains consistency with the Yamigishi (1997) study, and since
it is a less familiar scale it may have decreased the possibility of
participants remembering their previous responses when completing the
second questionnaire (i.e., when they returned one week later).
Participants were asked to rate the risk for the average Australian
rather than themselves, in order to reduce the influence of personal
experience and increase reliance on the statistics.
3 Results
The year format resulted in higher mean risk ratings than the day
format, averaged across salience conditions and the eleven causes of
death. Table 2 shows the mean risk ratings for each cause, all
of which had higher risk ratings for the year format.
| Table 2: Incidence rates and mean
risk ratings for day and year formats, averaged across salience
conditions. Scale anchored at 0 = “no risk at
all” and 25 = “highest possible
risk.” |
| | Number of | Mean risk |
| | deaths | rating |
|
Cause of death | Day | Year | Day | Year |
| Cancer | 100 | 36,500 | 18.90 | 19.42 |
| Heart disease | 70 | 25,500 | 17.90 | 18.71 |
| Stroke | 30 | 11,000 | 16.25 | 16.54 |
| Respiratory diseases | 16 | 5,800 | 13.40 | 14.19 |
| Pneumonia | 10 | 3,600 | 12.19 | 12.63 |
| Diabetes | 8 | 2,900 | 11.40 | 13.27 |
| Heart failure | 7 | 2,500 | 14.38 | 15.60 |
| Motor vehicle accidents | 6 | 2,200 | 13.13 | 16.38 |
| Renal failure | 5 | 1,800 | 9.54 | 10.50 |
| Homicide | 3 | 1,100 | 9.06 | 10.98 |
| AIDS | 1 | 350 | 9.42 | 11.63 |
| MEAN | | | 13.23 | 14.53 |
| (SD) | | | (4.31) | (3.48) |
A 3 x (2 x 11) repeated measures ANOVA was conducted, with factors of
salience (control, numerical, temporal), format (day, year) and cause
of death (11 causes). A significant main effect of format was found,
such that the year format resulted in higher risk ratings than the day
format (F(1,45) = 6.17, p = 0.017). As expected when
using different incidence rates, there was also a significant main
effect of cause (F(1,10) = 36.00; p =
0.000), indicating that the overall risk ratings varied amongst the
different causes of death. The rank order of risk ratings amongst the
11 causes generally followed the rank order of incidence rates, with
the exception of motor vehicle accidents and heart failure, which are
ranked as relatively more risky than their incidence rates suggest.
The reason for this is not immediately obvious, but it could be
related to lower ratings for diabetes, pneumonia and respiratory
diseases, which may be perceived as less obvious causes of death.
There was no significant main effect of salience, and there were no
significant interactions.1
There was no significant main effect of order (day versus year format
first), nor did this factor interact with any other factors.
On an individual level, almost two-thirds of the participants (30 out
of 48) gave higher average year ratings than day ratings, with a mean
difference of 3.57 (SD = 2.34) on the 26 point risk rating scale. The
minority of participants (18 out of 48) who gave higher average day
ratings than year ratings had a smaller mean difference of 2.49 (SD =
1.70). The higher ratings were not related to the order in which
participants completed the two formats, suggesting that there are
effects in both directions amongst the individual participants. This
can be illustrated using a P-P plot, based on individual
paired t-tests of day versus year ratings (11 causes x 2
formats). By definition of the p-value, if
H0 is true, then the set of 48 individual
p-values will be uniformly distributed from 0 to 1, with
equal numbers and distribution in each direction. The cumulative
probability for each observed p-value was calculated such
that higher day ratings were equal to p/2 (i.e., small
p-values approach 0) and higher year ratings were equal to
1-(p/2) (i.e., small p-values approach 1). Figure 1
shows the expected cumulative probabilities against the observed
cumulative probabilities for H0. The graph clearly
shows that the distribution of observed p-value
probabilities deviates from the expected uniform distribution line,
such that both directions have more participants at the extreme ends
(i.e., small p-values) than would be expected by chance
(particularly in the year higher than day direction, approaching 1 on
the expected cumulative probability axis), and that overall there are
more participants in the year higher than day direction (those above
0.5 on the expected cumulative probability axis).
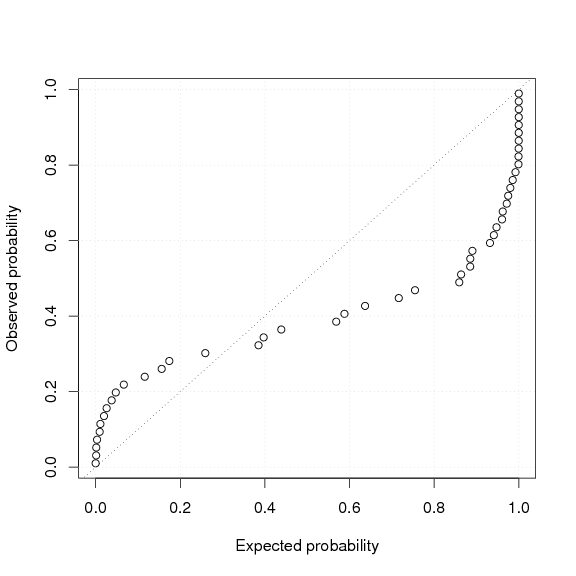
| Figure 1: P-P plot of the observed cumulative probability of
individual p-values against the expected cumulative probability.
Under the null hypothesis that risk ratings are equal in the day and
year formats, a uniform distribution along the identity line is
expected. Points above 0.5 on the expected cumulative probability
axis indicate year higher than day, with the smallest p-values
approaching 1. Points below 0.5 on the expected cumulative
probability axis indicate day higher than year, with the smallest
p-values approaching 0. |
4 Discussion
The present research set out to investigate how different statistical
formats influence risk perception. The aim was to find out which of
two opposing effects — ratio bias or temporal construal — is more
influential in judgments of risk, and whether this can be affected by
a salience manipulation. The key finding was that when the ratio bias
and the temporal construal effect are in opposition, the ratio bias
appears to dominate. Across all eleven causes of death, risk ratings
were higher when a “year” format (which had a large frequency based
on a longer time period) was used than when a “day” format (which
had a small frequency based on a shorter time period) was used. This
was despite the fact that the incidence rates in the two formats were
equivalent. Increasing the salience of numerical or temporal
information through font and order within each statistic had no effect
on the relative influence of the ratio bias and temporal construal.
The present experiment replicates and extends the findings of
Yamagishi (1997) by demonstrating that a temporal frame (e.g., day or
year) is neglected in a similar way to a numerical frame (e.g., per
100 or 10,000) when rating the risk of causes of death. However, our
failure to find an overall effect of temporal construal is
inconsistent with the findings of Chandron and Menon (2004). The
different pattern of results may be due to the way in which temporal
construal is manipulated. In their study, Chandron and Menon presented
participants with risk descriptions of the form “Every year a
significant number of people die from…”; this contrasts with
the numerical information we provided (e.g., “Every year 100
people die from …”). It is possible that the effect of
temporal construal demonstrated by Chandron and Menon (2004) was due
to the ambiguous nature of the phrase “a significant number of
people.” In their discussion the authors acknowledge this
possibility, suggesting that the temporal information may have been
used as an indication of what “a significant number” meant. The
numerical figures included in the present study overshadowed the
effect of temporal construal for the majority of participants.
Although the term “ratio bias” usually refers to a numerical ratio,
the effect found in the present experiment can be explained in the
same way, using the heuristic of anchoring and adjustment (Tversky &
Kahnemann, 1974).2 According to this account,
the number of deaths is used as a cue to ratings of risk, with
insufficient adjustment for the frame (day or year). In this case, the
statistic was framed in a temporal form, but the same principle can be
applied to any statistic where a frequency is given in context —
successful operations per hospital, faulty goods per order, robberies
per suburb, etc. Any frame may be neglected in a similar way to the
more typical numerical denominator, leading to greater perceived risk
whenever a larger frame (and therefore higher frequency) is used.
The finding that the ratio bias persists even when placed in opposition
to the effect of temporal frame adds to existing evidence of its strong
influence on judgment and decision making. The ratio bias has been
shown to cause non-optimal decisions in both forced choice tasks
(Denes-Raj & Epstein, 1994) and more realistic scenarios, such as
choosing which job to apply for (Alonso & Fernandez-Berrocal, 2003).
Monetary incentives to make better choices may reduce the number of
non-optimal choices within subjects, but even this does not prevent the
effect of the ratio bias (Dale, Rudski, Schwarz & Smith, 2007).
From the individual results, the finding that some participants show the
opposite effect (i.e., risk ratings higher in the day format) could be
related to individual differences in numeracy (Reyna & Brainerd,
2008). When a mixed numerical/temporal ratio is provided, the less
numerate participants may focus more on the non-numerical information
(day or year) as a cue to risk ratings, leading to a bias towards the
closer temporal proximity of the day format. Again, this could be
attributed to anchoring and adjustment (Tversky & Kahnemann, 1974),
where there is a focus on one part of the statistic with insufficient
adjustment for the accompanying information.
The ratio bias has practical implications for risk communication. A
simple incidence rate may be the first awareness some people have of a
particular risk, so increasing risk perception by using the most
effective format could be the difference needed for them to take
further action. Although a sense of risk may not itself be sufficient to
modify behaviour, it is considered in most health models to be a
necessary precondition (Weinstein, 1993; Van der Pligt, 1996), so
anything that increases perceived risk, such as using a larger frame to
describe incidence rates, will also increase the chance of reaching
positive behavioural outcomes. Although this perspective assumes that
increasing risk perception is desirable, it should be acknowledged that
such an effect may not always be accurate or beneficial (such as
overweighting the risk of side effects from a vaccine, when avoiding
the vaccine is actually more risky). In addition, using mixed
statistics where the frequency and its frame are in different forms
(such as numerical/temporal) may lead to reduced accuracy in risk
perception as a result of individual biases towards one form over the
other.
Further research on the use of different statistical formats, including
non-numerical frames, would enable a better understanding of its effect
on risk perception.
References
Alonso, A., & Fernandez-Berrocal, P. (2003). Irrational decisions:
attending to numbers rather than ratios. Personality and
Individual Differences, 35, 1537–1547.
Australian Bureau of Statistics (2003). Causes of death, Australia 2003.
http://www.abs.gov.au
Chandron, S. & Menon, G. (2004). When a day means more than a year:
effects of temporal framing on judgments of health risk.
Journal of Consumer Research, 31, 375–389.
Dale, D., Rudski, J., Schwarz, A. & Smith, E. (2007). Innumeracy and
incentives: A ratio bias experiment. Judgment and Decision
Making, 2, 243–250.
Denes-Raj, V. & Epstein, S. (1994). Conflict between intuitive and
rational processing: When people behave against their better judgment.
Journal of Personality & Social Psychology, 66, 819–829.
Gigerenzer, G. & Hoffrage, U. (1995). How to improve Bayesian reasoning
without instruction: Frequency formats. Psychological Review,
102, 684–704.
Hampson, S. E., Andrews, J. A., Barckley, M., Lichtenstein, E. & Lee,
M. E. (2000). Conscientiousness, perceived risk, and risk-reduction
behaviors: A preliminary study. Health Psychology, 19,
496–500.
Kirkpatrick, L., & Epstein, S. (1992). Cognitive-Experiential
Self-Theory and subjective probability: Further evidence for two
conceptual systems. Journal of Personality and Social
Psychology, 63, 534–544.
Newell, B. R., Mitchell, C. J. & Hayes, B. K. (in press). Getting
scarred and winning lotteries: Effects of exemplar cuing and
statistical format on imagining low probability events. Journal
of Behavioral Decision Making.
Pinto-Prades, J. L., Martinez-Perez, J. E. & Abellán-Perpiñán, J.
M. (2006). The influence of the ratio bias phenomenon on the
elicitation of health states utilities. Judgment and Decision
Making, 1, 118–133.
Reyna, V. F. & Brainerd, C. J. (2008). Numeracy, ratio bias, and
denominator neglect in judgments of risk and probability.
Learning and Individual Differences, 18, 89–107.
Slovic, P., Monahan, J. & MacGregor, D. G. (2000). Violence risk
assessment and risk communication: The effects of using actual cases,
providing instruction, and employing the probability versus frequency
formats. Law and Human Behavior, 24, 271–296.
Trope, Y. & Liberman, N. (2003). Temporal construal.
Psychological Review, 110, 403–421.
Tversky, A. & Kahneman, D. (1974). Judgment under uncertainty:
Heuristics and biases. Science, 185, 1124–1131.
Tversky, A. & Kahneman, D. (1981). The framing of decisions and the
psychology of choice. Science, 211, 453–458.
Van der Pligt, J. (1996). Risk protection and self protective behaviour.
European Psychologist, 1, 34–43.
Weinstein, N. D. (1993). Testing four competing theories of
health-protective behavior. Health Psychology, 12, 324–333.
Yamigishi, K. (1997). When a 12.86% mortality is more dangerous than
24.14%: Implications for risk communication. Applied Cognitive
Psychology, 11, 495–506.
This document was translated from LATEX by
HEVEA.
