KEY WORDS: utility elicitation, cost-effectiveness, person
trade-off, analog scale, decision analysis, consistency checks,
transfer of training.
Measures of judged utility can provide valuable input to public policy decisions, including those about medical care. For example, comparison of the utility of medical treatment to its cost can yield a benefit/cost ratio, which can be used to allocate scarce resources where they are most effective. Utility measures require human judgment, and several methods have been proposed to elicit judgments from respondents (Baron, 1997; Kaplan, 1995; Torrance, 1986; Ubel et al., 1996).
We focus here on three of these methods, analog scale (AS), magnitude estimation (ME), and person trade-off (PTO). At issue are whether these methods can yield internally consistent responses, whether they agree with each other, and how their internal consistency and agreement can be improved. As we discuss later, these methods can be seen as representative of two general types of methods in common use, one involving direct utility judgments and the other involving matching responses in hypothetical decisions.
In the analog scale (AS) method, respondents assign numbers to conditions on a scale with the ends clearly defined. Typically one end is death and the other is normal health, but here we use conditions other than death in most studies. Because we define the worse end of the scale as 100 and normal health as 0, we speak of the scale as measuring disutility rather than utility.
The AS is simple to use and explain. In principle, it is justified by the idea of difference measurement. That is, differences among numbers should be ordered according to judged differences among the conditions to which they correspond (Krantz et al., 1971, sect. 4.2). In practice, AS produces disutilities that seem excessively high: conditions are judged to be closer to the worse end of the scale than other methods or intuition suggests. For example, Ubel et al. (1996) asked subjects, ``You have a ganglion cyst on one hand. This cyst is a tiny bulge on top of one of the tendons in your hand. It does not disturb the function of your hand. You are able to do everything you could normally do, including activities that require strength or agility of the hand. However, occasionally you are aware of the bump on your hand, about the size of a pea. And once every month or so the cyst causes mild pain, which can be eliminated by taking an aspirin.'' The AS ratings implied a disutility of 8 on a scale where normal health is 0 and death is 100. In other words, the cyst was judged about 1/12 as bad as death.
We show here that at least part of the problem is that subjects ignore instructions to consider differences, so their numbers conflict with their own judgment of differences. Instead, they seem to follow some sort of psychophysical function anchored on normal health, a function with a slope that flattens as distance from normal health increases. Such functions have been found even for ratings of monetary losses, where economic theory predicts, if anything, the reverse kind of curvature (Galanter & Pliner, 1974; Kahneman & Tversky, 1979).
Note that AS asks the subject to make a judgment about a less bad condition using a worse condition as a standard with a disutility of 100, so numerical responses are less than 100. In magnitude estimation (ME), we ask the subject to compare the worse condition to the less bad condition, to which we assign a disutility of 10. Responses are thus greater than the disutility of the standard. We reserve the term ME for comparisons of worse to less bad, following the usage of others (Kaplan, 1995, Richardson, 1994), although the term has been used for what we call AS as well. The ME task is discussed in the literature on decision analysis (Fischer, 1995; von Winterfeldt & Edwards, 1986, ch. 8) and it has a long and continuing history in psychophysics (Birnbaum, 1978; Fagot & Pokorny, 1989; Stevens, 1951). Our interest in ME is primarily as a way of checking the consistency of AS. If both AS and ME represent utilities the direction of judgment should not matter: if condition A is judged to be half as bad as B, then B should be judged twice as bad as A. Although a utility representation implies such inversion consistency, inversion consistency is not sufficient for a utility representation. (For example, inversion consistency will hold for any power transform of utility; see Baron & Ubel, 1999).
The third method of interest here is the person trade-off (PTO). In one version of the PTO, the subject is asked how many people have to be cured of condition B to do just as much good as curing (say) 10 people of condition A. (A is worse than B, so the subject's response is larger than 10.) PTO has been advocated because it seems most directly relevant to policy decisions about allocation of resources (Nord, 1995). However, it yields results that are internally inconsistent. In particular, when subjects compare conditions B and A (as above) and conditions C and B, we should be able to predict their comparison of C and A by multiplying the first two utilities. For example, if curing 20 Bs is as good as 10 As and curing 30 Cs is as good as 10 Bs, then curing 60 Cs should be as good as 10 As. Ubel et al. (1996) found that the C-A comparison is less extreme than predicted on the assumption that subjects were equating numbers on the basis of utilities. We call this result ratio inconsistency (following Baron & Ubel, 1999; Ubel et al. called it ``multiplicative intransitivity'').
Ubel et al., and others such as Nord et al. (1995), have suggested that subjects are making PTO judgments on the basis of considerations of fairness that go beyond equating total utility for the two groups of patients. Two types of additional fairness considerations are relevant. First, subjects want to give patients equal opportunity for treatment regardless of their condition. This principle would lead to judgments of equal disutility for all conditions; hence, 100 people cured of Condition A would always be equivalent to 100 people cured of Condition B, regardless of the nature of A and B. Second, subjects want to treat the worse condition first (Ubel et al., 1998a,b). If A were worse than B, then subjects asked how many people cured of A is equivalent to 100 people cured of B would answer 1. Both of these principles could lead subjects to pay too little attention to the relative seriousness of A and B. They would thus tend to give the same answers for any comparison, and this would result in ratio inconsistency.
An alternative explanation of internally inconsistent results for PTO is that of scale distortion, much like that described for AS. We know of no previous results that would predict the direction of this distortion, and, in principle, it could go in either direction, of under- or over-responsiveness to differences among conditions.
Subjects could make PTO judgments in different ways. In one, they think about the decision problem of allocating resources. Fairness considerations could come into play. In the other, they evaluate the conditions (as they do in AS or ME) and use this evaluation to infer the PTO judgment. For example, if they judge A to be twice as bad as B, they would infer that curing 50 people of A is equivalent to curing 100 people of B. We test this possibility by comparing two ways of presenting PTO judgments. In one, we present PTO judgments on their own. In the other, we present each PTO judgment immediately after an equivalent ME judgments. We use ME because the answer is larger than the standard, just as it is for the PTO question that we used.
The studies reported here have two main purposes. One is to demonstrate inconsistencies in the utility measures of interest. The second is to ask how these inconsistencies can be corrected in the process of elicitation. We thus examine both inconsistencies and the effects of training. Of particular interest is whether training will transfer to new cases and whether training in one sort of consistency will improve other measures of consistency as a byproduct. The latter result is expected if improvements in consistency also improve validity. By validity, we mean that the numbers are more representative of an internal scale that both honestly expresses subjects' judgments and has the form of a utility measure. Internal consistency does not imply validity, but inconsistency implies invalidity.
The results may shed light on utility judgment more generally, both in health contexts and other contexts. AS and PTO are two of the four methods most often discussed in the literature on utility elicitation (Kaplan, 1995), the other two being time-tradeoff and standard gambles. PTO is like the latter two methods because it asks subjects for a number that makes two options equally preferred in a hypothetical decision. AS is like methods sometimes used in multi-attribute decision analysis. Decision analysts (e.g., Keeney & Raiffa, 1993) usually recommend that analysis should not take initial judgments of utility at face value. Instead, the analysis should carry out consistency checks. Experiments of the sort we do here could thus show the need for such checks in health utility elicitation and also shed light on the effectiveness of such checks in decision analysis.
The experiment asked several questions about the nature and sources of disagreement among methods of utility estimation:
1. Do ME and PTO yield comparable results? Ubel et al. (1996) found that AS consistently yielded larger disutilities (closer to death) than did PTO. But PTO could be affected by fairness considerations, as argued earlier. Worst-first, in particular, would lead to smaller disutilities (closer to normal health) when they are estimated with PTO. ME would not have this problem, since it is a direct judgment, not a decision about distribution.
To compare ME and PTO, we made sure that the numerical scales were the same. In PTO, we asked how many people needed to be cured of a less severe condition to equal the benefit of curing 10 people of the more severe condition. Thus, PTO indifference points were 10 or greater. We also used 10 as the standard for ME judgments.
Subjects could also think about PTO in terms of disutilities. They could answer questions about ratios of people as if they were questions about ratios of disutility. We gave PTO twice, the second time (called PTO2) interleaved with ME. That is, each ME item was followed by a PTO item with the same two conditions This was to encourage subjects to think about the PTO in this way. We could compare these judgments to PTO judgments presented alone. We also asked subjects whether they objected to thinking about the PTO in this way.
2. Is ratio inconsistency present in ME, as well as in PTO? If ratio inconsistency is the result of fairness only, it should be absent in ME, but found in PTO.
3. Does it matter whether the PTO asks about the benefit of curing people or the harm of not curing them? We used two versions of PTO: one involved curing people (which we abbreviate as PTO), and the other involved not curing people (leaving them uncured, PTO-NotCure). These versions would differ if subjects think of equal opportunity as more important for losses (PTO-NotCure) than for gains (PTO), or the reverse. Equality would express itself as relatively close and high disutilities inferred from PTO: in the extreme, if subjects said that curing 10 people of each condition was equivalent to curing 10 people of the worst condition, then all conditions would have an implied disutility of 1 on a scale with 1 as the maximum.
4. Does the AS method yield disutility judgments that are too large? To test this, we asked subjects to compare the effect of becoming deaf on normal people and blind people. If subjects think that deafness is worse in people who are blind, then they should judge blindness as less than half as bad as blindness plus deafness.
5. Can asking about differences reduce the bias in AS judgments? We gave the AS method by itself and in a condition that requested the subject to compare differences (as in #4) before completing the scale (AS-CompDiffs).
6. How does ME compare to AS? These two measures may be considered as different ways of asking about the same ratio. In AS, the worse condition is the standard of comparison; in ME, the less bad.
Twenty subjects, paid $6/hour (raised to the nearest dollar), completed this questionnaire and others at their own pace in a quiet room. Most were students at the University of Pennsylvania and Philadelphia College of Pharmacy and Science.
The questionnaire had two forms, in the following orders:
| First form | Second form |
| PTO | PTO-NotCure |
| PTO-NotCure | PTO |
| AS | AS-CompDiffs |
| ME and PTO2 (interleaved) | ME and PTO2 (interleaved) |
| AS-CompDiffs |
Ten subjects completed each form. The two orders served to counterbalance the order of PTO and PTO-NotCure, and they also differed in whether AS-CompDiffs was presented after AS (without the difference comparison questions). We saw no point in presenting this form of AS after AS-CompDiffs in the second order.
The questionnaire began with a list of the conditions and their
standard abbreviations given to the subjects, and, in brackets,
the abbreviations we use here:
One-blind [B]: blindness in one eye.
Blind [BB]: blindness in both eyes.
One-deaf [D]: deafness in one ear.
Deaf [DD]: deafness in both ears.
One-blind-and-one-deaf [BD]: blindness in one eye and deafness in
the opposite ear.
Blind-and-deaf [BBDD]: blindness and deafness.
It then reminded the subject of the limitations resulting from each condition, and it said, ``In the questions to follow, suppose that these conditions begin in adults from ages 20 to 60, and they do not get better by themselves. People with them do not differ in sex, age, or any other characteristics. You should rate these conditions for the average person.''
Here are the introductions and a sample item from each condition:
Curing people [PTO]Suppose that, in a given state, the Medicaid budget is increased so that the state can pay for certain expensive procedures, which it did not pay for before. These procedures can cure people of these disorders. The state cannot pay for everything, but it wants to do the most good with what it has. So it wants to determine the benefits of curing different numbers of people of different conditions. It will then try to get the most benefit for its money.
IN THIS PART, YOUR ANSWERS SHOULD ALL BE GREATER THAN 10.
Curing 10 people with Blind does as much good as curing people with One-blind.
...
Not curing people: leaving them uncured [PTO-NotCure]
Suppose that, in a given state, a new Medicaid program is put into effect, but funds are limited. The state will be unable to pay for certain expensive procedures, which can cure people of these disorders. The state must decide which procedures not to cover. It must decide how much harm is done by not covering certain procedures, so it can do the least harm possible within its budget.
IN THIS PART, YOUR ANSWERS SHOULD ALL BE GREATER THAN 10.
Leaving 10 people Blind does as much harm as leaving people One-blind.
...
Analog scale [AS]
Put each of the following conditions on the following scale by drawing an arrow from the condition name to the point on the scale where it goes. Differences on the scale should reflect differences between the conditions. For example, a difference of two units should be twice as great as a difference of one unit. Do Blind first, then Deaf, and so on. [The questionnaire listed all the conditions using full descriptions - which were ordered BB, DD, B, D, BD - and it provided a vertical scale marked with ``No impairment'' at the top end, called 0, and ``Blind-and-deaf'' at the bottom, called 100.]
...
Ratios [PTO-ME, magnitude estimation with person tradeoff interleaved]
In this part, fill in the blanks with ratios. You do not need to use whole numbers. You can use decimals or fractions. After each ratio question, answer the corresponding question about the benefits of curing people.
Blind is times as bad as One-blind.
Curing 10 people with Blind does as much good as curing people with One-blind.[Additional items compared DD with D, BD with B, BD with D, and BBDD with BB, DD, B, D, and BD.]
...
Comparisons [AS-CompDiffs]
Person A is normal and becomes Deaf. Person B is Blind and becomes Deaf. For which person is it worse to become Deaf? Or are these effects equally bad? (Circle one)?
A B equally bad
Person A is normal and becomes One-deaf. Person B is One-blind and becomes One-deaf. For which person is it worse to become One-deaf? Or are these effects equally bad? (Circle one)?
A B equally bad
The answers to these questions should be consistent with the following scale. That is, a bigger change should correspond to a larger interval on the scale, and an equal change should correspond to equal intervals. Please bear this in mind. [The Analog Scale followed.]
Comparison of methods. ME and PTO methods yielded smaller disutilities than AS methods, and ME was smaller than PTO. Mean disutilities of each condition are shown in Exhibit 1. Items with disutilities of one or greater are excluded from all analyses (e.g., giving 10 or less as a response in PTO methods - 5.6% of responses overall).
To compare methods, we computed, for each method, the mean disutility (on a 0-1 scale) of the conditions common to methods being compared. Although the level of this measure has no natural interpretation, it allows us to compare measures, with each response contributing equally in proportion to its utility.
ME disutilities were significantly smaller than all other measures except for PTO-ME (the PTO condition interleaved with ME; p = .003 or better by t test). PTO and PTO-NotCure did not differ.
AS and AS-CompDiffs did not differ, either within the subjects who did both or between the groups that did one or the other first. The comparison manipulation thus had no overall effect. We formed a single variable for whichever was done first. Mean disutilities of this variable were larger than those of all other methods (p = .001 or better).
Consistency with difference judgments. Before AS-CompDiffs, the questionnaire asked for direct comparisons of differences between states. In response to the first of these questions, 19 of 20 subjects said that it was worse for a Both-blind person to become Both-blind-Both-deaf than for a normal person to become Both-blind. Yet, when the subjects completed the scale after answering this question, 19 out of 20 assigned a disutility of at least .5 to Both-blind, and 16 of these were .6 or higher. (The difference in proportions is of course significant at p < .0005.) Subjects therefore did not bring their judgments of differences to bear on their disutility judgments, despite the instructions to do so.
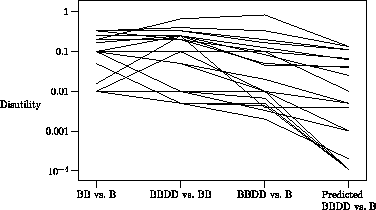
Ratio inconsistency. In PTO (all versions) and ME, judgments were inconsistent. (We could not assess consistency for AS in this study.) For example, the mean ME disutility of One-blind as a proportion of Blind is 0.138, the disutility of Blind as a proportion of Blind-and-Deaf is 0.174, and the disutility of One-blind as a proportion of Blind-and-deaf is 0.106, which is higher than 0.024, the product of the first two utilities. Exhibit 2 shows the individual subject data for this comparison.
For PTO, PTO-NotCure, PTO2, and ME, we measured ratio inconsistency for each set of judgments of this sort for which it could be measured by taking the product of the first two utilities, dividing by the third, and taking the log. The overall ratio inconsistency measure for each method was the mean of these four scores. All of these means were less than zero (p = .033 or better). They did not differ significantly from each other.
Relation of PTO to ME. A PTO-ME condition was interleaved with the ME condition, to determine whether subjects found it acceptable to make person tradeoff judgments in terms of utility ratios. Nine (out of 20) subjects produced PTO-ME utilities identical to their ME utilities, even though both of these differed from their initial PTO utilities, two subjects produced PTO-ME utilities that were farther (by a factor of at least four) from their PTO utilities than from their ME utilities, and two subjects had identical utilities for all three judgments. These 13 subjects evidently had no objection to making PTO judgments in terms of ratios. Three subjects produced PTO-ME utilities closer to their PTO utilities than to their ME utilities. These subjects evidently resisted the idea of making PTO judgments in terms of ratios. Two of the remaining four subjects did not produce utilities less than 1 for PTO-ME, and two did not produce such answers for PTO. Of the latter two, one had ME utilities that matched the PTO-ME utilities and one did not. In sum, only four subjects resisted responding to the PTO-ME task as if it were a magnitude estimation, and 14 seemed to accept the idea. Exhibit 3 shows the disutilities for PTO-NotCure, PTO, PTO-ME, and ME.
Although thinking of the PTO task as magnitude estimation may have made the task easier, it only increased (nonsignificantly) the ratio inconsistency of the judgments. This result is inconsistent with the hypothesis that ratio inconsistency in PTO results from fairness principles. Rather, ratio inconsistency is more easily explained in terms of insufficient distinctions among different conditions. Subjects may anchor on one condition when they rate others, then adjust insufficiently for the differences among conditions.
AS vs. ME. Disutilities based on AS were larger in all comparisons than those based on ME; all comparisons were significant. Although small effects resulting from the direction of comparison occur in psychophysical tasks (Fagot, 1981; Fagot & Pokorny, 1989), the magnitude of these differences suggests a different mechanism, which may have to do with the fact that the scale is unbounded in ME.
This experiment examined further the conflict between AS and PTO. It included tests of ratio inconsistency in AS as well as PTO. And it included two PTO conditions, one in which the more severe condition was the standard and subjects had to decide how many people needed to be cured of the less severe condition to bring equal benefits, and another PTO condition (PTO-Rev) in which the less severe condition was the standard and subjects had to state a PTO indifference point for the more severe condition. This allowed us to ask whether the discrepancy between AS and ME was found in other tasks in which the standard differed.
The experiment used a face-to-face interview procedure rather than written administration, although some subjects answered the same questions in written form for comparison. The interview attempted to train the subjects to make internally consistent judgments. Subjects were told both about ratio inconsistency and about comparison of intervals in AS. That is, they were encouraged to make sure that differences between the numbers they assigned in AS reflected their ordering of differences between conditions. For example, a subject who thought that the difference between Both-Blind and Blind-and-Deaf was greater than that between No-impairment and Blind should give Both-Blind a rating of less than 50 on the AS in which Blind-and-Deaf was assigned 100. The interview also trained subjects in ratio consistency.
We asked two questions about the effect of training. First, when subjects are induced to become more consistent, do they merely make their numbers follow the rules without worrying about whether the numbers still reflect their honest judgment? Or, alternatively, are judgments sufficiently flexible so that they can be made mathematically consistent while still being honest? Decision analysts claim that consistency checks usually do not violate the respondent's best judgment, for example: ``... if the consistency checks produce discrepancies with the previous preferences indicated by the decision maker, these discrepancies must be called to his attention and parts of the assessment procedure should be repeated to acquire consistent preferences. ... Of course, if the respondent has strong, crisp, unalterable views on all questions and if these are inconsistent, then we would be in a mess, wouldn't we? In practice, however, the respondent usually feels fuzzier about some of his answers than others, and it is this degree of fuzziness that usually makes a world of difference. For it then becomes usually possible to generate a final coherent set of responses that does not violently contradict any strongly held feelings'' (Keeney & Raiffa, 1993, p. 271). Such checks can even improve the perceived validity of numerical judgments (e.g., Keeney & Raiffa, 1993, p. 200). In this experiment, we wanted to test whether this was true of our respondents, who are more like representatives of the public than like the experts that Keeney and Raiffa typically used for decision analysis.
Second, if training improves consistency within a method - AS or PTO - does it also increase agreement between the disutilities inferred from the two different methods? If so, then it would be more likely that the modified disutilities were converging on some true utility judgment, not necessarily the truth about the conditions themselves but, rather, about the subjects' judgments of the disutility of these conditions. We might expect such convergence if the subject has an internal scale of disutility, which obeys the consistency requirement, but the subject distorts this scale when expressing it through certain kinds of questions. When the distortions are removed, different kinds of questions will tap the same underlying scale. This is the theoretical claim made by the idea of scale convergence in psychophysics (Birnbaum, 1978).
Following the same introduction as in the last experiment - which referred to a health insurer's need to measure the benefit of various interventions - half the subjects began with PTO and half with AS. Twenty-two subjects were interviewed, and 26 completed a written form of the same items (without any consistency checks, so that they answered each question only once). Order had no effect and is not discussed further. Data from an additional five subjects in the written condition were excluded because these subjects consistently answered PTO questions backward, giving numbers smaller than the standard when larger numbers were expected. (In the interview, such responses were quickly corrected and subjects had no problem after one correction. These answers are of interest in their own right but are not examined further here. See Lochhead, 1980, for a related phenomenon.)
The PTO was essentially the same as the PTO condition of Experiment 1, except that it included only the following comparisons: BBDD vs. BB; BBDD vs. DD; BB vs. B; DD vs. D; BBDD vs. B; and BBDD vs. D. (Again, one letter means one eye or ear and two letters mean both.) These comparisons permitted two ratio consistency checks, one involving BBDD, BB, and B, and the other involving BBDD, DD, and D. The first group of items were of the form, ``Curing 10 patients with Both-blind-Both-deaf is equivalent to curing patients with Both-blind.''
In addition, in a second group of items, called PTO-Rev, the form of the comparison was reversed, e.g., ``Curing patients with Both-blind-Both-deaf is equivalent to curing 100 patients with Both-blind.'' This meant that the response was a utility measure for the second term, on a 0-100 scale defined by No-impairment and the first term, respectively. The responses from this judgment were thus directly comparable to those from the AS. PTO-Rev included only four comparisons: BBDD vs. BB; BBDD vs. DD; BB vs. B; and DD vs. D. We could not assess ratio inconsistency here.
The AS condition asked for judgments on individual scales instead of all at once, so as to make the two methods more comparable. So, for example, the subject was asked, ``Where does Both-blind go on the following scale?'' and a horizontal line was provided, divided into tenths by tick marks, with 0 and ``No-impairment'' at the left and 100 and ``Both-blind-Both-deaf'' on the right. A separate scale of this sort was used for each of the other comparisons listed for the PTO, allowing the same ratio inconsistency checks.
Half of the interviewed subjects in each order (AS first, PTO first) were given an introduction to the consistency checks to be carried out, before they did the task. The introduction was designed to counteract any tendency of the subject to resist the consistency checks on the grounds that the initial judgments should have been correct. The introduction simply explained the checks to be done but then told the subject not to think about them when making the judgments. It had no effect, so we shall not describe it further.
After each task, all subjects were given a set of consistency checks specific to that task, and they were then asked to redo the task, if necessary more than once, in order to try to make their judgments consistent. Most subjects redid the entire task only once, but so many made minor changes along the way that we did not attempt to count the number of times the task was done; we used only the final judgments in each task as our data.
The ratio inconsistency check for AS was read to the subject as follows (the letters referring to the subject's answers), for one of the two checks:
From your answers, we can conclude that being Both-blind is A% as bad as being Both-blind-Both-deaf, and being One-blind is C% as bad as being Both-blind. So the badness of being One-blind compared to Both-blind-Both-deaf should be C% of A% or CA%. But you said E%.This was followed by a check for differences, as follows:This would create a problem for the insurer. To determine the badness of being One-blind relative to Both-blind-Both-deaf, they would not know which answer to use. They might not always have time to ask everyone all three questions about all combinations of conditions.
Try to make your numerical answers consistent. Can you do this and still have them reflect your true opinions about the conditions? (If not, why not?)
Which is greater, the difference in badness between having No Impairment and being Both-blind, or the difference in badness between being Both-blind and being Both-blind-Both-deaf? A should be more than 50 if you think that the first difference is larger, and it should be less than 50 is you think that the second difference is larger.This difference check was repeated for the deafness items, and the interviewer explained the tests as needed. The consistency checks for the PTO were essentially the same, but modified as needed. The ratio inconsistency check was done for the PTO items only, and the difference check was done for the PTO-Rev items only.[The test was repeated for One-blind vs. Both-blind.]
If these tests don't work, it would create a problem for the insurer. If they had to decide whether to treat some number of people with one condition or twice as many people with another condition, your answers about which difference is greater would imply one thing, but your numerical answers would imply another.
Try to make your numerical answers consistent. Can you do this and still have them reflect your true opinions about the conditions? (If not, why not?)
The PTO check also began with a question about whether PTO could be interpreted as a ratio: ``Does the number of people matter, or the ratio? For example, you said that curing 10 people with Both-blind-Both-deaf is equivalent to curing A people with Both-blind. So curing 1 person with Both-blind-Both-deaf is equivalent to curing A/10 people with Both-blind. Is that right? [If not, explain that the insurer wants numbers that it can use this way. It doesn't know how many people have each condition.]''
Likewise, the PTO-Rev check began with: ``Now we might think of your answers as measures of how bad each condition is. The number of Both-blind-Both-deaf people that are equivalent to a condition in 100 people is proportional to how bad that condition is. Do you see any reason why the insurer shouldn't interpret your answers this way?''
Twenty-two subjects were interviewed, 12 with and 10 without the introduction to the consistency checks (which, as we said, had no effect). Eleven of the 22 did PTO, PTO-Rev, and AS, and 11 did the reverse. In addition, 26 subjects (14 AS-first, 12 PTO-first) completed the scales in a written form only, without an interviewer, and without consistency checks. This allowed us to test for effects of the presence of an interviewer on consistency in the first set of items. Subjects were solicited as in Experiment 1.
Acceptability of consistency. Essentially all of the interviewed subjects found it acceptable to try to make their judgments consistent, although not all of them managed to succeed in doing so.
Mean disutility and ratio inconsistency before consistency checks. The interview vs. paper subjects did not differ significantly in the measures common to both groups, so we combined the groups for the analysis of effects before the consistency checks. (This lack of difference suggests that interviewing as such does not change performance, except for the opportunity to correct backward interpretation of the PTO.)
Mean disutilities on the comparisons common to all three tasks were .47 for AS, .35 for PTO, and .40 for PTO-Rev. All differences were significant at p = .030 or better by t test. Of particular interest is the difference for PTO-Rev and PTO. What is common to the tasks with smaller disutilities (ME, vs. AS in Experiment 1, and PTO, vs. PTO-Rev) is that they both involve high numerical responses. At least part of the effect, then, may be explained in terms of a tendency to assign higher numerical responses to the condition to which a number is assigned, whether this condition is the worse condition or the less bad condition.
Ratio inconsistency was measured as before, as the log of the product of the smaller steps divided by the larger step (e.g., BBDD vs. BB times BB vs. B, divided by BBDD vs. B - the product being taken of this and the corresponding measure for deafness). Before the consistency checks, ratio inconsistency was not significantly different from zero for AS (mean -0.10), but was less than zero for PTO (mean -0.72, t44 = 2.70, p = .010). The difference was significant (t42 = 2.34, p = .024). These results are consistent with those of Experiment 1, where we found negative ratio inconsistency for PTO and did not examine ratio inconsistency in AS. Although the mean ratio inconsistency in AS was neither positive or negative, only 15% of the subjects made perfectly consistent judgments.
Effect of consistency checks. Consistency checking increased agreement between AS and PTO, and it decreased the absolute value of ratio inconsistency. Exhibit 4 shows the mean disutilities for the interview subjects only, for purposes of comparison.
Although effects of the checks (initial vs. second) were small, they did reduce ratio inconsistency. The absolute value of ratio inconsistency for the interview subjects decreased from 0.29 to .07 for AS (t19 = 3.01, p = .007) and from 1.06 to .46 for PTO (t18 = 3.19, p = .005). The mean ratio inconsistency for AS was still not significantly different from zero, after the checks. The mean ratio inconsistency for PTO was not significantly different from zero after the checks, and it changed significantly (from -.35 to .17 for the 18 subjects with complete data, p = .027) from before to after.
The mean disutility in AS decreased from .37 before the checks to .34 after (for the mean of all items, p = .031). They did not affect the means for PTO or PTO-Rev.
The measures agreed with each other after the consistency manipulation more than before. To measure disagreement between two measures, we computed the mean absolute value of the differences of the utilities of all the items common to the measures. (We excluded cases in which more than 2 items were missing from AS or PTO or more than one from comparisons involving PTO-Rev.) Disagreement between AS and PTO was .187 before and .151 after the consistency checks (t17 = 2.46, p = .012, one-tailed). Disagreement between AS and PTO-Rev was .169 before and .155 after (n.s.). Disagreement between PTO and PTO-Rev was .117 before and .111 after (n.s.). Although only one of the three before-after comparisons was significant, the mean of all three measures was also significant (t19 = 2.11, p = .024), and the nonsignificant results were those with the fewest data.
To determine the source of the reduced disagreement between AS and PTO, we regressed the inconsistency reduction on four predictors, two for each measure: the reduction in (absolute value of) ratio inconsistency for AS and PTO; and the decrease in mean disutility for AS and PTO. The overall regression was significant (p = .035). The only significant predictor was the reduction in the AS mean (b = .62, p = .011). These results suggests that the reduced inconsistency between AS and PTO was the result of bringing down the excessively high disutilities expressed in AS. This may have resulted from the difference training. Although ratio consistency training was effective, its effect apparently did not contribute to the reduced disagreement.
Experiment 3 asks whether training effects in consistency checking can transfer between two different methods, AS and ME. Such transfer effects are consistent with the view that training could lead to more accurate expression of judgments on an underlying utility scale. The experiment compared trained groups to control groups with no training.
Subjects were 60 undergraduate or graduate students from the University of Pennsylvania, mean age 21.2 (33 males and 27 females). Two additional subjects made obvious careless mistakes, and one yielded utilities for magnitude estimations that were more than two orders of magnitude smaller than the closest other subject (with ratios on the order of a million). These three subjects were not included. Subjects were paid $6, and the experiment took less than an hour.
Analog Scale (AS) and Magnitude Estimation (ME) were used in four questionnaires. AS-before and ME-before represented the AS and ME before the consistency check. AS-after and ME-after represented the AS and ME after the consistency check. The analog scale was printed with normal condition as its left end and a worse health state as its right end. Subjects were asked to put a third, less serious, condition in the appropriate position on the scale. ME questions simply asked subjects how many times worse one condition was than another.
Two sets of health conditions were included in AS-before, ME-before, AS-after and ME-after, one dealing with paralysis and the other with sensory losses. The paralysis items were: one arm (A), one leg (L), both arms (AA), both legs (LL), and both arms and legs (AALL). Death (X) was also included. The sensory items were blindness of one eye (B), complete blindness (BB), deafness in one ear (D), complete deafness (DD), blindness and deafness (BBDD), and death (X). Each group (AS-before, ME-before, AS-after, ME-after) had 9 questions, three groups of three, with each group allowing a check for ratio consistency. The ratio inconsistency tests in the paralysis items were based on the products of the following ``first two items'' compared to the third item. Each item shows the standard on the right.
| First two items | Compared to | |
| Paralysis items: | ||
| AALL/LL | LL/L | vs. AALL/L |
| X/AA | AA/A | vs. X/A |
| X/AALL | AALL/LL | vs. X/LL |
| X/AALL | AALL/L | vs. X/L |
| Sensory items: | ||
| BBDD/BB | BB/B | vs. BBDD/B |
| X/DD | DD/D | vs. X/D |
| X/BBDD | BBDD/BB | vs. X/BB |
| X/BBDD | BBDD/B | vs. X/B. |
Subjects completed AS-before and ME-before, then did a consistency check either on AS-before (AS-before experimental group) ME-before (ME-before experimental group) or neither (control group), and finally completed AS-after and ME-after. Assignment of content (sensory vs. paralysis) to before/after was counterbalanced, as was order of the 9 items in each group (which was otherwise random).
The instruction for all groups began: ``The purpose of this study is to evaluate different public health care programs. Suppose the Department of Health in a state must choose a new policy to prevent various illness. The decision would depend on factors such as the seriousness of each illness, the cost of prevention, the amount of budget, etc. The basic idea for making decision is that we want to get the most benefit from the money spent. The following questions are used for measuring the badness of each health state. Imagine that all the patients are college students.'' Then subjects were given specific instruction and examples about how to complete AS and ME.
The consistency check was given to the two experimental groups. The check varied according to the difference of inconsistency. For example: ``In question B you used number X to indicate the badness of Paralysis of one arm when the badness of Paralysis of both arms was 100. That meant you thought Paralysis of one arm was X% as bad as Paralysis of both arms. Following this inference, you thought Paralysis of both arms was Y% as bad as Death. According to the method for calculating utility, your evaluation for Paralysis of one arm was (X ·Y)% as bad as Death. Now look at question I, in which you thought Paralysis of one arm was Z% as bad as Death. Z% was quite different from (X ·Y)%. This would create a problem for decision makers, who are responsible for deciding which health care program to use. They would not know which answer, the direct or indirect one, represented your true opinion, and they don't have time to ask every respondent why such inconsistency existed. Please take a moment to think about this problem and whether you can be more consistent?''
The consistency check increased consistency within each method (AS and ME), transferred to the untrained method, and increased agreement between the two methods. Again, because subjects differed in the direction of their initial ratio inconsistency and because we wanted to use as many data as possible, we used the absolute value of the ratio inconsistency measure in the analysis of the data. (Because the measure was logarithmic, 0 indicated perfect consistency.)
Inconsistency decreased in the experimental groups and increased in the control group, but the increase was not significant. The best measure of a training effect is comparison of the decrease in inconsistency between the experimental and control groups. For the trained task (AS or ME), this difference was significant for each kind of training (t38 = 3.87, p = .0004, for AS; t38 = 3.15, p = .0031, for ME). For the untrained tasks, this difference was significant for AS (t38 = 2.23, p = .0320) but not for ME (t38 = 1.40, p = .1692). However, an overall test of transfer to the untrained task, combining both AS and ME (and averaging the two conditions in the control group), yielded a significant difference (t58 = 2.23, p = .0295). Moreover, the two experimental groups did not differ significantly in the change in the untrained task (t = 1.06). We can thus conclude that, in general, the training transferred to the other task, whichever task was trained. Transfer was not complete, however: the interaction between change in AS vs. ME and group (for the experimental groups) was significant (F1,38 = 4.62, p = .038).
Although we used the absolute value to look at training effects, we note that ratio inconsistency was in the same direction as previously found, with the product of the smaller differences too high relative to the larger difference (mean of .13 for AS-before, t59 = 5.30, p = .0000; .43 for ME, t59 = 6.71, p = .0000). The effects of training were also significant when we used the raw measure in place of the absolute value (t58 = 2.72, p = .0085, for trained task; t58 = 2.44, p = .0177, for untrained [transfer] task).
Our most important result concerns the effect of exposing subjects to consistency checks. We asked subjects to do two kinds of checks, one for difference comparison and one for ratio inconsistency. These checks reduced ratio inconsistency in all measures, reduced mean disutilities in AS, and reduced the disagreement among measures. Experiment 3 shows that this change is not just a function of repeated testing, although the effect here was limited to ratio inconsistency (because the other discrepancy was not trained). The increased agreement in Experiment 2 was apparently mediated, to some extent, by the reduction in mean disutilities for AS. This is consistent with the hypothesis that AS disutilities are generally too high, as in the case of the ganglion cyst cited in the introduction. The reduced disagreement suggests increased validity, and the apparent reason for it is consistent with our conclusion that AS disutilities are generally too high.
Increased agreement among measures as a result of inconsistency reduction in one of the measures suggests that inconsistency is a source of invalidity. Again, our interest here is in the validity of expression of an internal scale that has the properties of a utility scale (assume that such a scale exists), not with a true judgment of the utility of a condition. We suggest this procedure as a general method for studying utility elicitations of all sorts.
In addition to these effects of consistency checking, our findings confirmed earlier reports of disagreement among measures of disutility. AS disutilities were highest - as typically found - and ME disutilities were lowest, a new result. PTO was larger than PTO-Rev, suggesting that the numbers assigned to the subject of the comparison are high, relative to the standard, regardless of which condition is the standard (worse or less bad). One explanation of this result is that the scale is unbounded when the numbers are higher than those assigned to the standard, but it is bounded by zero when they are lower. Subjects may not want to get too close to zero.
The difference between PTO and ME was, for most subjects, not a matter of strong commitment: when the two judgmenuring, MEts were interleaved, most subjects thought it reasonable to make them agree. AS judgments were inconsistent with direct judgments of differences, and merely asking subjects to make the difference judgment before doing the AS task did not reduce this inconsistency.
We also found ratio inconsistency in PTO (as reported by Ubel et al., 1996) and in ME. The direction of the ratio inconsistency is that the most extreme judgments were not extreme enough. Either the disutility assigned to the least bad condition relative to the worst one is not low enough, or the disutility assigned to the intermediate conditions is not high enough, or both. Mean AS ratio inconsistency across subjects was not different from zero, but some subjects were inconsistent in each direction.
AS judgments are inconsistent with judgments of differences. Most subjects assign disutilities of more than .5 to blindness or deafness on a scale from no impairment (0) to blindness+deafness (1). Yet, the same subjects judge that the difference between no impairment and blindness or deafness is less than that between either blindness or deafness alone and both together. The latter judgment seems reasonable, since vision and hearing are, to some extent, substitutes in the economic sense. Either can be a means to communication, for example, and when both are absent communication becomes much more difficult. We therefore suspect that the AS disutility judgments are in fact too high. This fact may also help to reduce ratio inconsistency, by leaving more room for relatively low numbers to be assigned to one-eye blindness or one-ear deafness. AS may thus increase internal consistency at the expense of external validity.
AS is one of the easier methods to use. It is more highly correlated than other measures with questionnaire scales of health (Bosch & Hunink, 1996), perhaps because it is less prone to error based on misunderstanding. High correlations, however, can be based on a correct ordering of conditions, even if the numbers assigned are generally too high or too low. Our results suggest that they are too high. But the results also suggest that appropriate instruction can substantially increase the validity of the responses.
Our study leaves several questions unanswered, and we are pursuing these in current research:
1. How do our results depend on the direction of the scale? Our questions all concerned disutility, using normal health as the reference point. Conceivably, the excessively high disutilities resulting from AS could result from a convex utility function in the domain of losses, and the use of normal health as a reference point could encourage such a perception. This is unlikely to be the whole story, since Ubel et al. (1996) also found that AS yielded larger disutilities, and they used death as the implied reference point.
2. What are the sources of the inconsistency between AS and ME and between PTO and PTO-Rev? It seems that subjects tend to give numbers that are too high, regardless of whether the worse condition or the less bad condition serves as the standard of comparison.
3. What are the causes of ratio inconsistency, and how is it reduced? Possibly, subjects anchor on earlier judgments when making later ones, so that their later judgments are not different enough from the earlier ones. Ratio inconsistency decreases after the consistency check, but we do not know why. In particular, we do not know whether subjects learn anything that would improve their judgments even when they cannot themselves carry out the consistency check.
Baron, J., & Ubel, P. A. (1999). `Inconsistencies in person-tradeoff and difference judgments of health-state utility', Manuscript.
Birnbaum, M. H. `Differences and ratios in psychological measurement', In N. Castellan & F. Restle (Eds.), Cognitive theory, (Vol. 3, pp. 33-74). Hillsdale, NJ: Erlbaum, 1978.
Bosch, J. L., & Hunink, M. G. M. 'The relationship between descriptive and valuational quality-of-life measures in patients with intermittent claudication', Medical Decision Making, 16 (1996), 217-225.
Fagot, R. F. `A theory of bidirectional judgments', Perception and Psychophysics, 30 (1981), 181-193.
Fagot, R. F., & Pokorny, R. `Bias effects on magnitude and ratio estimation power function exponents', Perception and Psychophysics, 45 (1989), 221-330.
Fischer, G. W. `Range sensitivity of attribute weights in multiattribute value models', Organizational Behavior and Human Decision Processes, 62, (1995), 252-266.
Galanter, E., & Pliner, P. `Cross-modality matching of money against other continua', In H. R. Moskowitz et al. (Eds.), Sensation and Measurement, pp. 65-76. Dordrecht: Reidel, 1974.
Houston, D. A., Sherman, S. J., & Baker, S. M. `The influence of unique features and direction of comparison on preferences', Journal of Experimental Social Psychology, 25 (1989), 121-141.
Kahneman, D., & Tversky, A. `Prospect theory: An analysis of decisions under risk', Econometrica, 47 (1979), 263-291.
Kaplan, R. F. `Utility assessment for estimating quality-adjusted life years', in F. A. Sloan (Ed.), Valuing health care: Costs, benefits, and effectiveness of pharmaceuticals and other medical technologies, pp. 31-60. New York: Cambridge University Press, 1995.
Keeney, R. L., & Raiffa, H. Decisions with multiple objectives. New York: Cambridge University Press, 1993 (originally published by Wiley, 1976).
Krantz, D. H., Luce, R. D., Suppes, P., & Tversky, A. Foundations of measurement (Vol. 1). New York: Academic Press, 1971.
Lochhead, J. `Faculty interpretations of simple algebraic statements: The professor's side of the equation', Journal of Mathematical Behavior, 3 (1980), 30-37.
Nord, E. `The person trade-off approach to valuing health care programs. Medical Decision Making, 15 (1995), 201-208.
Nord, E., Richardson, J., Kuhse, H., & Singer, P. `Who cares about cost? Does economic analysis impose or reflect social values?' Health Policy, 34 (1995), 79-94.
Richardson, J. `Cost-utility analysis: What should be measured?' Social Science and Medicine, 39 (1994), 7-21.
Stevens, S. S. `Mathematics, measurement and psychophysics', in S. S. Stevens (Ed.), Handbook of Experimental Psychology, pp. 1-49. New York: Wiley, 1951.
Torrance, G. W. (1986). Measurement of health-state utilities for economic appraisal: A review. Journal of Health Economitine Weeks does market research, 1-30
Ubel, P. A., Loewenstein, G., Scanlon, D., & Kamlet, M. `Individual utilities are inconsistent with rationing choices: A partial explanation of why Oregon's cost-effectiveness list failed.' Medical Decision Making, 16 (1996), 108-116.
Ubel, P. A., Nord, E., Gold, M., et al. `Improving value measurement in cost-effectiveness analysis', Manuscript (1998a).
Ubel, P. A., Spranca, M., DeKay, M., et al. `Public preferences for prevention versus cure: What if an ounce of prevention is worth only an ounce of cure?' Medical Decision Making, 18 (1998b), 141-148.
von Winterfeldt, D., & Edwards, W. Decision analysis and behavioral research. Cambridge University Press, 1986.
1. Without taking the log, equivalent errors in the numerator and denominator of the ratio could lead to a positive mean error. For example, if the disutility of B relative to BBDD (B/BBDD) is 25% too high on half the trials and the product of BB/BBDD and B/BB is 25% too high on the other half, the mean ratio would be the mean of 5/4 and 4/5, which is 1.025 rather than 1. The distribution of the log ratio is also approximately normal, although the ratio itself has a skewed distribution.
2. Ratio inconsistency went in both directions for both measures,
even though the mean value of ratio inconsistency was negative
for PTO before the consistency checks. The checks were effective
in reducing ratio inconsistency regardless of its direction.
Exhibit 1.
Disutilities inferred from each method for each comparison. For
example, .38 for BB/BBDD in PTO means that subjects thought that,
on the average, curing about 26 people of BB was as good as
curing 10 people of BBDD (since .38 is about 10/26).
(Abbreviations: B = blind in one eye, BB = blind, BBDD = blind and
deaf, etc.; PTO = person tradeoff, PTO-NotCure = person tradeoff
for not curing, ME = magnitude estimation, AS = analog scale,
PTO-ME = person tradeoff interleaved with ME, AS-CompDiffs =
analog scale following comparison of differences.
| Method | ||||||
| PTO | PTO-NotCure | AS | ME | PTO-ME | AS-CompDiffs | |
| BB/BBDD | .38 | .36 | .78 | .17 | .26 | .75 |
| DD/BBDD | .35 | .37 | .66 | .15 | .25 | .73 |
| B/BBDD | .24 | .22 | .34 | .11 | .17 | .33 |
| D/BBDD | .21 | .20 | .23 | .09 | .14 | .24 |
| BD/BBDD | .31 | .28 | .52 | .12 | .13 | .48 |
| B/BB | .31 | .32 | .14 | .23 | ||
| D/DD | .33 | .32 | .15 | .25 | ||
| BD/BB | .44 | .45 | .29 | .34 | ||
| BD/DD | .43 | .43 | .28 | .32 | ||
Exhibit 2.
Each subject's disutilities for magnitude estimation (ME) of
blindness (BB) relative to one-eye blindness (B), blindness plus
deafness (BBDD) relative to blindness, one-eye blindness relative
to blindness plus deafness, and the prediction of the last
measure from the first two, assuming ratio consistency. The
utility scale is logarithmic. Each line represents the data from
one subject.

Exhibit 3.
Each subject's disutilities for PTO-NotCure, PTO-Cure,
PTO-Cure2 (with ME), and ME. Each line is one subject.
Subjects with missing data on intermediate points are excluded.
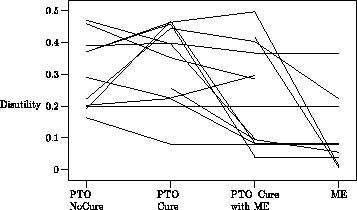
Exhibit 4.
Mean disutilities for interviewed subjects. ``2'' means after
the consistency checks. Abbreviations are the same as in Exhibit
1.
| Method | ||||||
| PTO | PTO-ME | PTO-Rev | PTO-Rev2 | AS | AS2 | |
| BB | .40 | .41 | .42 | .45 | .59 | .57 |
| DD | .30 | .34 | .34 | .34 | .45 | .44 |
| B/BB | .33 | .33 | .33 | .31 | .39 | .36 |
| D/DD | .30 | .30 | .33 | .36 | .33 | |
| B | .16 | .14 | .23 | .20 | ||
| D | .13 | .13 | .19 | .16 | ||
Exhibit 5.
Mean inconsistency (absolute value of log) and standard deviation
(in parentheses) before and after the consistency check.
| AS-before | ME-before | AS-after | ME-after | |
| Check on AS-before | .257 (.135) | .488 (.379) | .108 (.108) | .357 (.405) |
| Check on ME-before | .188 (.116) | .520 (.583) | .153 (.134) | .143 (.173) |
| Control | .216 (.177) | .477 (.487) | .242 (.199) | .604 (.521) |
Jonathan Baron is Professor of Psychology, University of Pennsylvania. A third edition of his book Thinking and deciding (Cambridge University Press) is expected this year.
Dallas Brennan is a researcher and writer on contemporary
cultural politics and mass media. She works regularly in Trinidad
and the United States and is based in New York City.
Peter Ubel is Assistant Professor, General Internal Medicine,
University of Pennsylvania. His book Pricing life: Why
it's time for health care rationing is published by MIT Press.
Christine Weeks does market research at Brintnall and Nicolini,
in Philadelphia.
Zhijun Wu is a graduate student in computer science at Temple
University.
1 This research was supported by N.S.F. grant SBR95-20288 (Baron). Peter Ubel's work was supported by the Department of Veterans Affairs through a Career Development Award in health services research and by the Robert Wood Johnson Foundation's Generalist Physician Faculty Scholar Program. Send correspondence to Jonathan Baron, Department of Psychology, University of Pennsylvania, 3815 Walnut St., Philadelphia, PA 19104-6196, or (e-mail) baron@psych.upenn.edu. Peter Ubel is in the Center for Bioethics and the Veterans Administration Medical Center.