Arrhenius Kinetics Analysis
Background:
Chemical kinetics is the study of the rates of chemical reactions. In order to determine the relationship between the rate of reaction and temperature, Arrhenius studied data proposed by several scientists in the 1880s. In order to quantify how reaction rates depend on temperature, Arrhenius developed an expression to represent the data. This expression, rate=Ae-Ea/RT, is today considered the Arrhenius equation.
Purpose:
The purpose of this analysis is to verify that the Arrhenius equation is an accurate way to quantify the dependence of reaction rates on temperature.
Analysis:
In order to analyze the correspondence of the Arrhenius equation to the data of investigators Hecht and Conrad, the reaction rate data was compiled in Excel and two graphs were constructed. The first graph (Figure 1) reflects the relationship between temperature and reaction rate. The second graph (Figure 2) reflects the relationship between the inverse temperature and the natural log of reaction rate. For each graph, a trend line was fit to the data points and an equation displayed on the graph.
Figure 1: Rate of reaction versus temperature for the reaction of ethoxide with methyl iodide
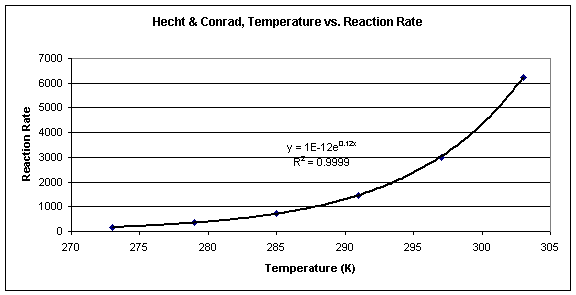
The graph in Figure 1 represents the relationship between reaction rate and temperature, where reaction rate increases with increasing temperature, approximately doubling for every 10-degree rise in temperature. This trend can be expressed as an exponential function, y = e-Ea/Rx, where y is the rate of the reaction and x is the temperature in Kelvin.
Figure 2: Natural log of reaction rate versus inverse temperature for the reaction of ethoxide with methyl iodide
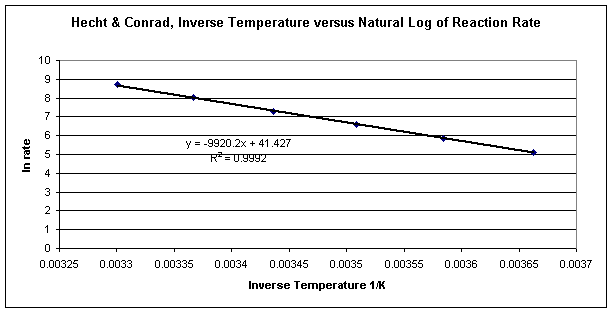
The graph in Figure 2 demonstrates a linear relationship between inverse temperature and the natural log of reaction rate. The equation for the trendline is in the form of y = mx + b. This means that the ln rate = -Ea/R (1/T) + ln A, where the slope of the line is –Ea/R and the y-intercept is equal to the natural log of constant A.
To determine the activation energy, Ea, multiply the slope of the line –9920.2 by the known constant R, 8.314 J/K, to obtain the equivalent of 82474.88 J or 82.47488 kJ.
Conclusions:
As demonstrated in this analysis, the Arrhenius equation is adequate for demonstrating the effect of temperature on the rate of a chemical reaction. The Arrhenius equation not only describes how reaction rates change with increasing temperature but also can be used to predict activation energy, Ea, of a chemical reaction. The graph in Figure 2 represents the linear relationship between the natural log of reaction rate and inverse temperature. From this linear equation, in the form, y = mx + b, it was possible to calculate the activation energy for this particular reaction. The slope of the line, m, is equivalent to –Ea/R according to the natural log of the Arrhenius equation, ln rate = -Ea/R (1/T) + lnA. The activation energy was calculated to be approximately 82.5 kJ. According to the data analysis, the expression developed by Arrhenius to describe the relationship between temperature and rate of a chemical reaction is consistent with the experimental evidence on reaction rate collected by Hecht and Conrad.