| HOME |
PHYSICS BASICS |
fMRI BASICS |
fMRI & ADD/ADHD |
REFERENCES |
This page provides an
introduction to the basic principles of Magnetic Resonance Imaging,
MRI.
Click on the links below to be directed to any of these topics.
PURPOSE
NUCLEAR MAGNETIC RESONANCE, NMR
ATOMIC STRUCTURE
MAGNETIZATION
TYPES OF MAGNETS
PULSES
GRADIENTS
RADIO SIGNALS
K-SPACE
FOURIER TRANSFORM
Click on the links below to be directed to any of these topics.
PURPOSE
NUCLEAR MAGNETIC RESONANCE, NMR
ATOMIC STRUCTURE
MAGNETIZATION
TYPES OF MAGNETS
PULSES
GRADIENTS
RADIO SIGNALS
K-SPACE
FOURIER TRANSFORM
PURPOSE
NUCLEAR MAGNETIC RESONANCE, NMR
Return to top
ATOMIC STRUCTURE
Return to top
MAGNETIZATION
TYPES OF MAGNETS
Return to top
PULSES
Return to top
GRADIENTS
Return to top
RADIO SIGNALS
Return to top
K-SPACE
Return to top
FOURIER TRANSFORM
Magnetic resonance imaging, MRI,
provides images of body tissues and their chemical compositions with
exceptional clarity and with little risk of harm to the patient.
MRI uses magnetic fields and emits waves with a frequency in the radio
wave region. Thus it is a very safe method of imagining. It
is particularly useful for pregnant women, babies, and other patients
for whom other imaging methods such as x-rays are dangerous.
Ironically, MRI was originally known as Nuclear Magnetic Resonance
Imaging as it is a form of Nuclear Magnetic Resonance (NMR)
spectroscopy. The nuclear had to be dropped because the public
perception of the term nuclear was fearful.
Return
to topNUCLEAR MAGNETIC RESONANCE, NMR
The term resonance refers to
equivalent frequencies. When a magnetized species exists it can
absorb the energy associated with a magnetic field of equivalent
strength. Nuclear
magnetic resonance exploits the fact that
different protons when placed in a uniform magnetic field will "feel"
slightly different levels of magnetism based on their environment
within a molecule. This is due to a phenomenon called
shielding. Some protons feel less of the applied magnetic field
because they are in an electron rich environment and their attractions
to the electrons "shield" them from the applied
magnetic field. The opposite is also true of protons in an
electron deficient environment. Regardless, varying the strength
of an applied magnetic field can yield important information about the
structure of a particular species based on its response to these
varying fields. A species only absorbs those frequencies which
are resonant with their own frequency. Hence absorption of a low
frequency suggests a species which is heavily shielded where absorption
of a high frequency suggests a species which is not heavily
shielded. Often NMR is calculated in reference to a
particular compound. For example, tetramethylsilane (TMS)
is often used as the reference value. TMS is highly shielded and
the frequency of radiation which it absorbs is often set equal to 0 on
NMR instruments. Since the
frequency absorbed is proportional to the applied field the shift from
the standard is measured rather than the exact frequency. Protons
attached to or in close proximity to electron donating groups will be
more heavily shielded and absorb lower frequencies whereas protons in
proximity to electron withdrawing atoms or groups will be less shielded
and
absorb higher frequencies. Thus large shifts from the reference
suggest electron withdrawing groups and small shifts suggest electron
donating groups.
NMR instruments typically scan from high fields to low fields and hence the higher field absorptions are plotted nearer the origin of the graph and the lower are plotted further from the origin. An example of an NMR spectrograph is shown below. The hydrogens of the methyl, -CH3, group experience the most shielding and thus absorbs the lowest frequency radiation. The hydrogens of the ethyl and aromatic carbons experience less shielding respectively because they have less s character respectively. Their decreasing s character increases their electronegativity and thus draws electrons away from the hydrogens. This withdrawal of electrons from the hydrogens decreases shielding and thus increases the frequency of the absorbed radiation.
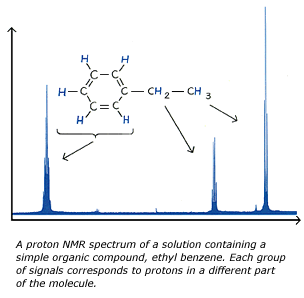
NMR instruments typically scan from high fields to low fields and hence the higher field absorptions are plotted nearer the origin of the graph and the lower are plotted further from the origin. An example of an NMR spectrograph is shown below. The hydrogens of the methyl, -CH3, group experience the most shielding and thus absorbs the lowest frequency radiation. The hydrogens of the ethyl and aromatic carbons experience less shielding respectively because they have less s character respectively. Their decreasing s character increases their electronegativity and thus draws electrons away from the hydrogens. This withdrawal of electrons from the hydrogens decreases shielding and thus increases the frequency of the absorbed radiation.

Return to top
ATOMIC STRUCTURE
The nucleus of an atom contains
protons, positively charged particles, and neutrons, neutrally charged
particles. Thus the nucleus has a net positive charge. Each
proton and neutron in the nucleus has its own spin. The net of
these spins is represented by spin number, I. I describes the
angular momentum of the spinning charge. If the mass number or
atomic number of the nucleus is odd then I has a non-zero value.
If the mass number and atomic number are both even then the spins of
the protons and neutrons will cancel each other out the nucleus will
have no net spin. The nucleus must possess an overall spin in
order for the species to respond to NMR.
As discussed above, nuclei which possess magnetic fields can be investigated by exposing them to varying magnetic fields. When the strength of the applied magnetic field is such that it is the same as that of the nucleus then the nucleus and the applied field are said to be in resonance. When this takes place the nucleus will absorb the magnetic radiation and this observation can be used to draw conclusions about the nucleus and its environment. Thus in order to use NMR it is essential that the nuclei possess a magnetic field and thus they must possess spin or have a non-zero I value. Common species with non-zero I values are H-1 and C-13. Unfortunately, C-12 and O-16 both have I=0 and are thereby useless with respect to NMR. Luckily, the human body contains large amounts of hydrogen-1 in water, lipids, and proteins. Thus hydrogen NMR can be very useful in making determinations about tissues and structures within the human body.
The allowed spins for a given value of I are given by the equation: 2I + 1. Thus when I=0 there is only one allowed spin state. NMR requires more than one possible spin state in order that the spin state could change. The frequency required to change the spin state or to cause a "flip" is what is detected by NMR. Both H-1 and C-13 have spin numbers I=1/2 thus they each have 2 possible spin states. When placed in an applied magnetic field of varying strength they will absorb the magnetic radiation when the frequency of that radiation is equivilent to that required to cause the nucleus to "flip" to its other spin state.
As discussed above, nuclei which possess magnetic fields can be investigated by exposing them to varying magnetic fields. When the strength of the applied magnetic field is such that it is the same as that of the nucleus then the nucleus and the applied field are said to be in resonance. When this takes place the nucleus will absorb the magnetic radiation and this observation can be used to draw conclusions about the nucleus and its environment. Thus in order to use NMR it is essential that the nuclei possess a magnetic field and thus they must possess spin or have a non-zero I value. Common species with non-zero I values are H-1 and C-13. Unfortunately, C-12 and O-16 both have I=0 and are thereby useless with respect to NMR. Luckily, the human body contains large amounts of hydrogen-1 in water, lipids, and proteins. Thus hydrogen NMR can be very useful in making determinations about tissues and structures within the human body.
The allowed spins for a given value of I are given by the equation: 2I + 1. Thus when I=0 there is only one allowed spin state. NMR requires more than one possible spin state in order that the spin state could change. The frequency required to change the spin state or to cause a "flip" is what is detected by NMR. Both H-1 and C-13 have spin numbers I=1/2 thus they each have 2 possible spin states. When placed in an applied magnetic field of varying strength they will absorb the magnetic radiation when the frequency of that radiation is equivilent to that required to cause the nucleus to "flip" to its other spin state.
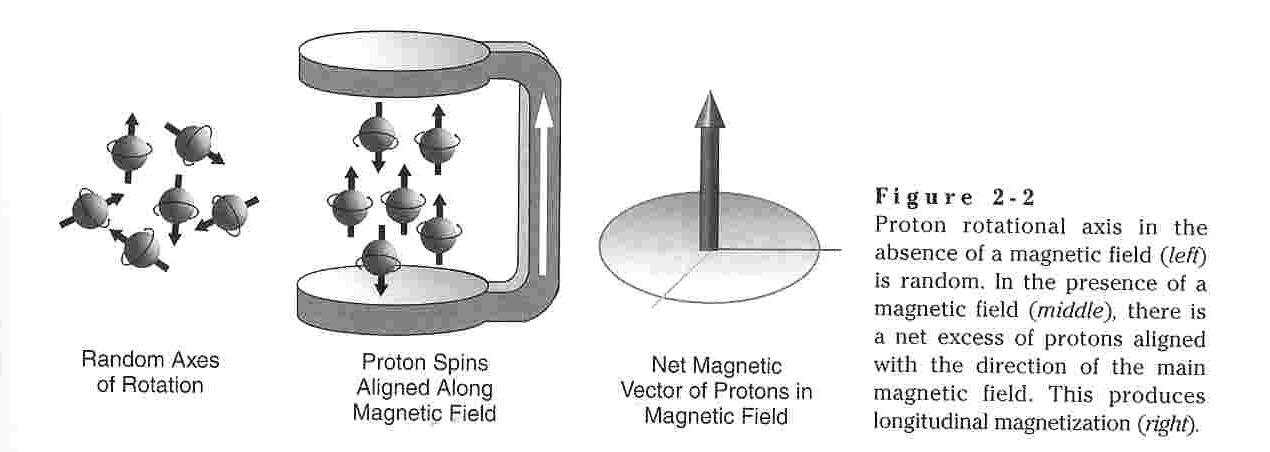
MAGNETIZATION
It
is fundamental that charged particles such as nuclei exhibit electric
fields. Electric fields induce magnetic fields and as such atomic
nuclei possess magnetic moments. As discussed above, for atoms
with non-zero values of I, these magnetic moments can take on more than
one orientation. In the absence of an outside force, these
varying spins states are degenerate (of equal energy.) Since
systems tend toward low energy in order to maximize stability the spin
state of the particles is random in the absence of an applied force as
each state is degenerate with the other. However, when atomic
nuclei are exposed to an applied magnetic field they will tend to
orient themselves as to minimize energy an maximize stability.
The diagrams below show how the lower energy orientation is that such
that the nuclei align their magnetic fields with the applied magnetic
field, that is N to N or S to S. The higher energy orientation is
that against the field with N to S and S to N.
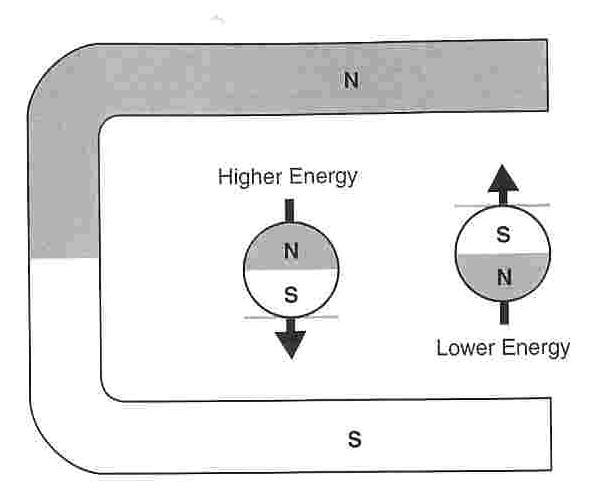
Thus when a magnetic field is applied many of the protons (nuclei) want to flip from the high energy state to the low energy state. By the law of conservation of energy, when this flip occurs the change in energy must be absorbed by or emitted to the environment. The change in energy will be exactly equal to the energy difference between the high and low energy states. Since a specific amount of energy is required, random “flipping” is unlikely. Generally it occurs because of interactions such as collisions with neighboring particles.
The next step is very similar to any other chemical equilibrium situation. If a far from equilibrium magnetic field is applied most collisions result in protons flipping from high to low energy states. This results in a buildup of low energy configurations. If a high energy proton is surrounded by a large number of low energy protons the effect of the applied magnetic field on the remaining high energy protons is decreased by their being surrounded by so many low energy protons and thus they do not flip to the low energy state. In summary, not all protons flip to the low energy state. However, at equilibrium there is still an excess of low energy spins to counter act the external magnetic field and the remaining high energy field. So, the system is said to be MAGNETIZED. The net excess is magnetization is known as longitudinal magnetization. The system’s approach to equilibrium is logarithmic. It is initially quick but slows as it reaches the equilibrium. The process is called magnetic recovery. The time is takes to achieve magnetic recovery is dependent on it T1 value and the strength of the magnetic field. The T1 value is dependent of the materials characteristics and is calculated as the time required to reach 63% magnetization. For reference purposes the T1 values of human body tissues range from 0.1 to 4.0 seconds. IV contrast is intended to lower the T1 value. The logarithmic function used to determine magnetic recovery time is : Mz=M0(1-e-t/T1)
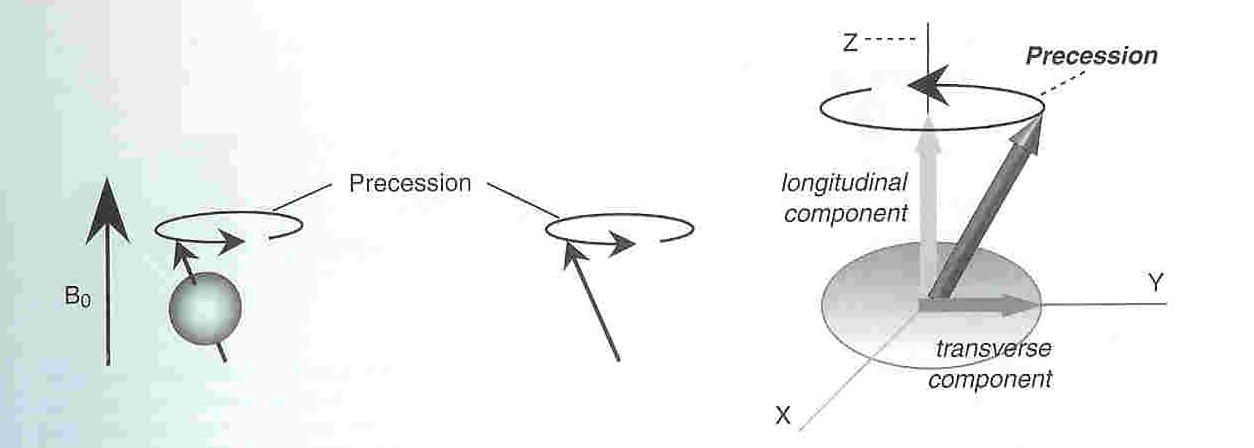
When a substance containing hydrogen, such as a human is placed is a strong magnetic field, B0, it quickly becomes magnetized as described above. Magnetized protons precess about their axis of rotation as shown in the diagram below. Since all protons have the same mass, all protons in a single magnetic field precess at the same frequency. This frequency is known as the Larmor frequency and is given by the equation: f=γB.
f = frequency of rotation, the number or rotations per second
γ= Larmor constant, "magnetogyric ratio,"
B= magnetic field strength
For protons, the Larmor constant is 42.58 millions of cycles per Tesla of of magnetic field. Thus a proton in a 1 Tesla magnetic field will precess at a rate of 42.58 million cycles per second and a proton in a 2 Tesla magnetic field will precess at a rate of 85 million cycles per second.
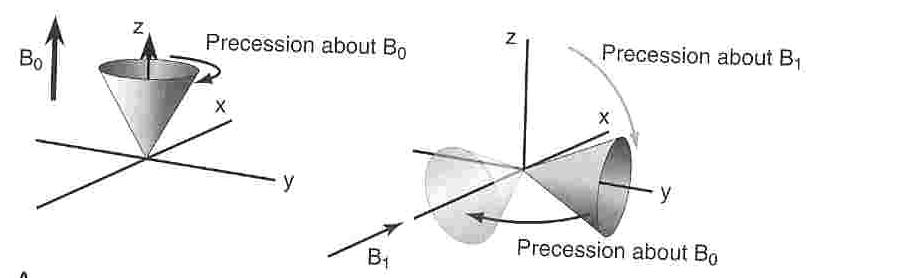
If a second magnetic field, B1, is applied perpendicular to the original magnetic field, and it rotates about the z axis as shown below at the same rate as the protons precess about the z axis. The fact that B1 rotates at a rate equal to the rate of precession of the protons causes the protons to feel as if the orientation of B1 is constant. However, since B1 is also a magnetic field the protons tend to precess about it as well. B1 is also governed by the Larmor equation and hence the degree to which the protons precess about it will be determined by its magnetic field strength. In short, when B1 is applied the cone of magnetization is flipped and rotated as the protons precess about the orthogonal magnetic field. The greater the magnitude of B1 and the longer it is "left on" the greater the degree of rotation of the protons. The other result of this rotation of the protons is that the protons are now oriented in the xy plane, perpendicular to the plane, along the z-axis, in which they lay with the energy minimized equilibrium. In fact, this perpendicular plane (xy) returns the protons to a situation in which an equal number of protons will be in the low and high energy states. Upon the removal of B1, the protons will return to their lower energy configuration oriented along the perpendicular z axis. Thus the protons return, or relax, to their magnetized state. It is this relaxation which is measured in MRI.
Return to top
Thus when a magnetic field is applied many of the protons (nuclei) want to flip from the high energy state to the low energy state. By the law of conservation of energy, when this flip occurs the change in energy must be absorbed by or emitted to the environment. The change in energy will be exactly equal to the energy difference between the high and low energy states. Since a specific amount of energy is required, random “flipping” is unlikely. Generally it occurs because of interactions such as collisions with neighboring particles.
The next step is very similar to any other chemical equilibrium situation. If a far from equilibrium magnetic field is applied most collisions result in protons flipping from high to low energy states. This results in a buildup of low energy configurations. If a high energy proton is surrounded by a large number of low energy protons the effect of the applied magnetic field on the remaining high energy protons is decreased by their being surrounded by so many low energy protons and thus they do not flip to the low energy state. In summary, not all protons flip to the low energy state. However, at equilibrium there is still an excess of low energy spins to counter act the external magnetic field and the remaining high energy field. So, the system is said to be MAGNETIZED. The net excess is magnetization is known as longitudinal magnetization. The system’s approach to equilibrium is logarithmic. It is initially quick but slows as it reaches the equilibrium. The process is called magnetic recovery. The time is takes to achieve magnetic recovery is dependent on it T1 value and the strength of the magnetic field. The T1 value is dependent of the materials characteristics and is calculated as the time required to reach 63% magnetization. For reference purposes the T1 values of human body tissues range from 0.1 to 4.0 seconds. IV contrast is intended to lower the T1 value. The logarithmic function used to determine magnetic recovery time is : Mz=M0(1-e-t/T1)

When a substance containing hydrogen, such as a human is placed is a strong magnetic field, B0, it quickly becomes magnetized as described above. Magnetized protons precess about their axis of rotation as shown in the diagram below. Since all protons have the same mass, all protons in a single magnetic field precess at the same frequency. This frequency is known as the Larmor frequency and is given by the equation: f=γB.
f = frequency of rotation, the number or rotations per second
γ= Larmor constant, "magnetogyric ratio,"
B= magnetic field strength

For protons, the Larmor constant is 42.58 millions of cycles per Tesla of of magnetic field. Thus a proton in a 1 Tesla magnetic field will precess at a rate of 42.58 million cycles per second and a proton in a 2 Tesla magnetic field will precess at a rate of 85 million cycles per second.
If a second magnetic field, B1, is applied perpendicular to the original magnetic field, and it rotates about the z axis as shown below at the same rate as the protons precess about the z axis. The fact that B1 rotates at a rate equal to the rate of precession of the protons causes the protons to feel as if the orientation of B1 is constant. However, since B1 is also a magnetic field the protons tend to precess about it as well. B1 is also governed by the Larmor equation and hence the degree to which the protons precess about it will be determined by its magnetic field strength. In short, when B1 is applied the cone of magnetization is flipped and rotated as the protons precess about the orthogonal magnetic field. The greater the magnitude of B1 and the longer it is "left on" the greater the degree of rotation of the protons. The other result of this rotation of the protons is that the protons are now oriented in the xy plane, perpendicular to the plane, along the z-axis, in which they lay with the energy minimized equilibrium. In fact, this perpendicular plane (xy) returns the protons to a situation in which an equal number of protons will be in the low and high energy states. Upon the removal of B1, the protons will return to their lower energy configuration oriented along the perpendicular z axis. Thus the protons return, or relax, to their magnetized state. It is this relaxation which is measured in MRI.

TYPES OF MAGNETS
Typically
MRIs are referred to as open or closed. This is controlled
primarily by the type of magnet being utilized. Open MRIs tend to
utilize permanent magnets, magnets in which the magnetic field is
oriented along an axis between the poles. The common drawback of
this arrangement has been the limits on the strength of these magnets
at about 0.5 tesla. Superconducting magnets coupled with low
temperatures have been able to overcome some of these challenges and
allow for open MRIs with magnetic field strengths of upto 1.0
tesla. Closed MRI are typically created by resistive
electromagnets, those which produce a magnetic field perpendicular to
an electric current flowing along an cylindrically coiled wire.
Return to top
PULSES
The
applied magnetic fields which cause protons to rotate at several
million times per second occur in the radio frequency range. Thus
the applied field which causes the flipping is a radio pulse.
These pulses are referred to as RF pulses. When an RF pulse is
continued long enough to allow for the spin to flip by 90O it
is called an 90O
RF pulse.
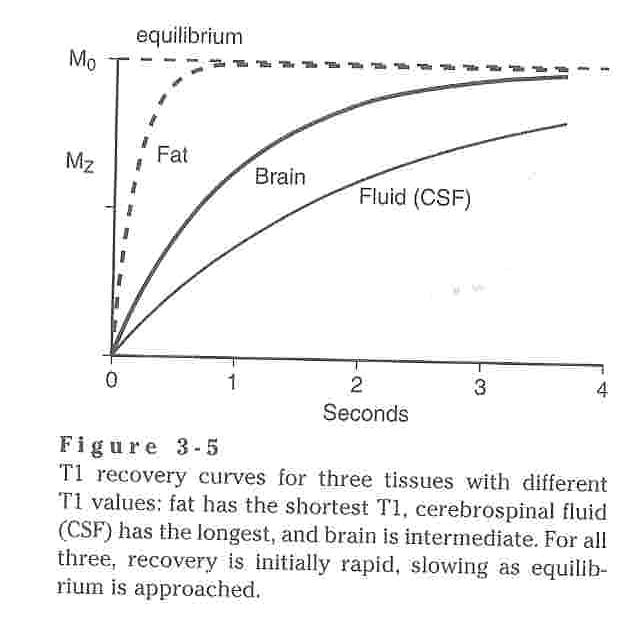
Water in human body tissue can be classified in one of two ways: free or bound. Free water is that which has a high degree of freedom of motion such as in urine and cerebrospinal fluid (CSF) where bound water is that which has much less freedom of motion such as in the brain and liver which have large intracellular surface areas. Since MR signals are those created when precessing protons which have been exposed to an RF pulse relax from the transverse plane back to the longitudinal plane, these MR signals require energy to be exchanged as the protons make this transfer from the higher energy transverse plane to the lower energy longitudinal plane and this energy generally comes from interactions, namely collisions, between the protons. Thus free water, with few intermolecular interactions, will undergo fewer collisions naturally, consequently requiring more energy, and thus relax less quickly than bound water. Thus urine and CSF have high T1 where the brain, fat, liver, etc. have low T1. Extending this logic to the MR signal, suppose a particular RF pulse is applied to a system and after a fixed amount of time it is discontinued. At this point the fat with the shorter T1 would be magnetized to a greater extent that the CSF and thus the MR signal it would produce upon relaxation would be stronger.
Another important consideration is repetition time between pulses, TR. If a 90O pulse is applied to a multiple tissue sample in which different portions of the sample have different T1 values, the portions with higher T1 values will return to longitudinal magnetization more slowly than those with shorter T1 values. Hence, at a given time following a 90O pulse, the longitudinal magnetization of the high T1 tissues will be less than that of the lower T1 tissues. This makes the MR signal of the longer T1 tissue darker than tissues with short T1. For example, spinal fluid in an MRI of the spine appears darker than the vertebrae. If the repetition time, TR, between pulses in constant than the signal contrast between tissues is steady and the contrast becomes pronounced and useful. On the flip side, if the TR is too short, the signal from all tissues becomes so low that very little contrast remains and thus the image becomes of little use. If a non-90O pulse is used some longitudinal magnetization remains and then more than one pulse will be require to get the system to a steady state. It is not really even possible to assume that a 90O pulse will necessarily produce perfect 90O rotation and hence many commercial scanners use dummy pulses to make sure a steady state is reached.
Water in human body tissue can be classified in one of two ways: free or bound. Free water is that which has a high degree of freedom of motion such as in urine and cerebrospinal fluid (CSF) where bound water is that which has much less freedom of motion such as in the brain and liver which have large intracellular surface areas. Since MR signals are those created when precessing protons which have been exposed to an RF pulse relax from the transverse plane back to the longitudinal plane, these MR signals require energy to be exchanged as the protons make this transfer from the higher energy transverse plane to the lower energy longitudinal plane and this energy generally comes from interactions, namely collisions, between the protons. Thus free water, with few intermolecular interactions, will undergo fewer collisions naturally, consequently requiring more energy, and thus relax less quickly than bound water. Thus urine and CSF have high T1 where the brain, fat, liver, etc. have low T1. Extending this logic to the MR signal, suppose a particular RF pulse is applied to a system and after a fixed amount of time it is discontinued. At this point the fat with the shorter T1 would be magnetized to a greater extent that the CSF and thus the MR signal it would produce upon relaxation would be stronger.

Another important consideration is repetition time between pulses, TR. If a 90O pulse is applied to a multiple tissue sample in which different portions of the sample have different T1 values, the portions with higher T1 values will return to longitudinal magnetization more slowly than those with shorter T1 values. Hence, at a given time following a 90O pulse, the longitudinal magnetization of the high T1 tissues will be less than that of the lower T1 tissues. This makes the MR signal of the longer T1 tissue darker than tissues with short T1. For example, spinal fluid in an MRI of the spine appears darker than the vertebrae. If the repetition time, TR, between pulses in constant than the signal contrast between tissues is steady and the contrast becomes pronounced and useful. On the flip side, if the TR is too short, the signal from all tissues becomes so low that very little contrast remains and thus the image becomes of little use. If a non-90O pulse is used some longitudinal magnetization remains and then more than one pulse will be require to get the system to a steady state. It is not really even possible to assume that a 90O pulse will necessarily produce perfect 90O rotation and hence many commercial scanners use dummy pulses to make sure a steady state is reached.
Return to top
GRADIENTS
Applying
a magnetic field gradient
along the axis about which the protons precess, in the direction of the
magnetic field, causes the precession frequency of the protons to
depend on their location along the axis. Generally this axis is
defined as the z axis. Images are divided into
slices in the perpendicular y plane and slice select gradients are
applied. Protons which precess in a constant magnetic field all
do so at the same frequency, given by the Armor equation. If a
varying magnetic field gradient is applied in the z direction (in
effect superimposed), the protons in that slice precess at frequencies
which correlate to their position. Then in sequence gradients are
applied orthogonally in the x and y directions to construct a 3D image.
Return to top
RADIO SIGNALS
The
frequency with which the protons precess is in the radio range and thus
is the frequency range of the MR signal.
Return to top
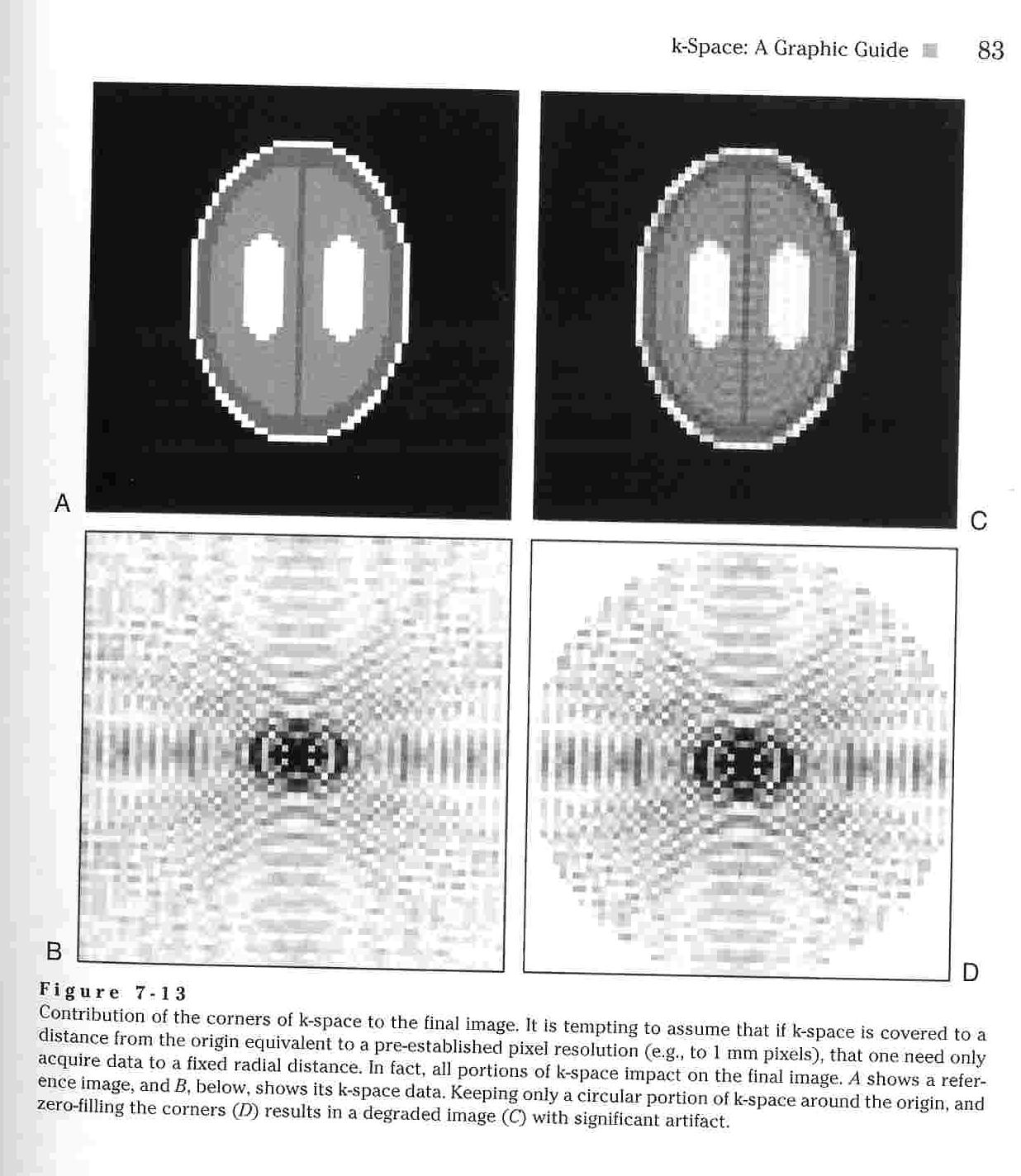
K-SPACE
The
k-space represents raw MRI signaling data prior to the Fourier
Transform being performed which gives the image. The k-space map
shows the most significant signals at the center and the less
significant signals at the edges. In fact, the edges are often
set equal to 0 to eliminate noise.
The following tutorial is an
excellent deeper explanation of k-space.

Return to top
FOURIER TRANSFORM
The
Fourier transform splits the radio signals into their constituent sin
curves each of which has a unique frequency. These frequencies
correlate to the protons in the tissues being studied. A computer
then translates these into images.
The following tutorial is an excellent deeper explanation of fourier transform.
Return to topThe following tutorial is an excellent deeper explanation of fourier transform.