Daniel Gomez

Front propagation in the shadow wave-pinning model, with K.Y. Lam and Y. Mori. Journal of Mathematical Biology (2023). (24 pages)
Multi-spike solutions to the one-dimensional subcritical fractional Schnakenberg System, with J. Wei and Z. Yang. Physica D: Nonlinear Phenomena (2023). (21 pages)
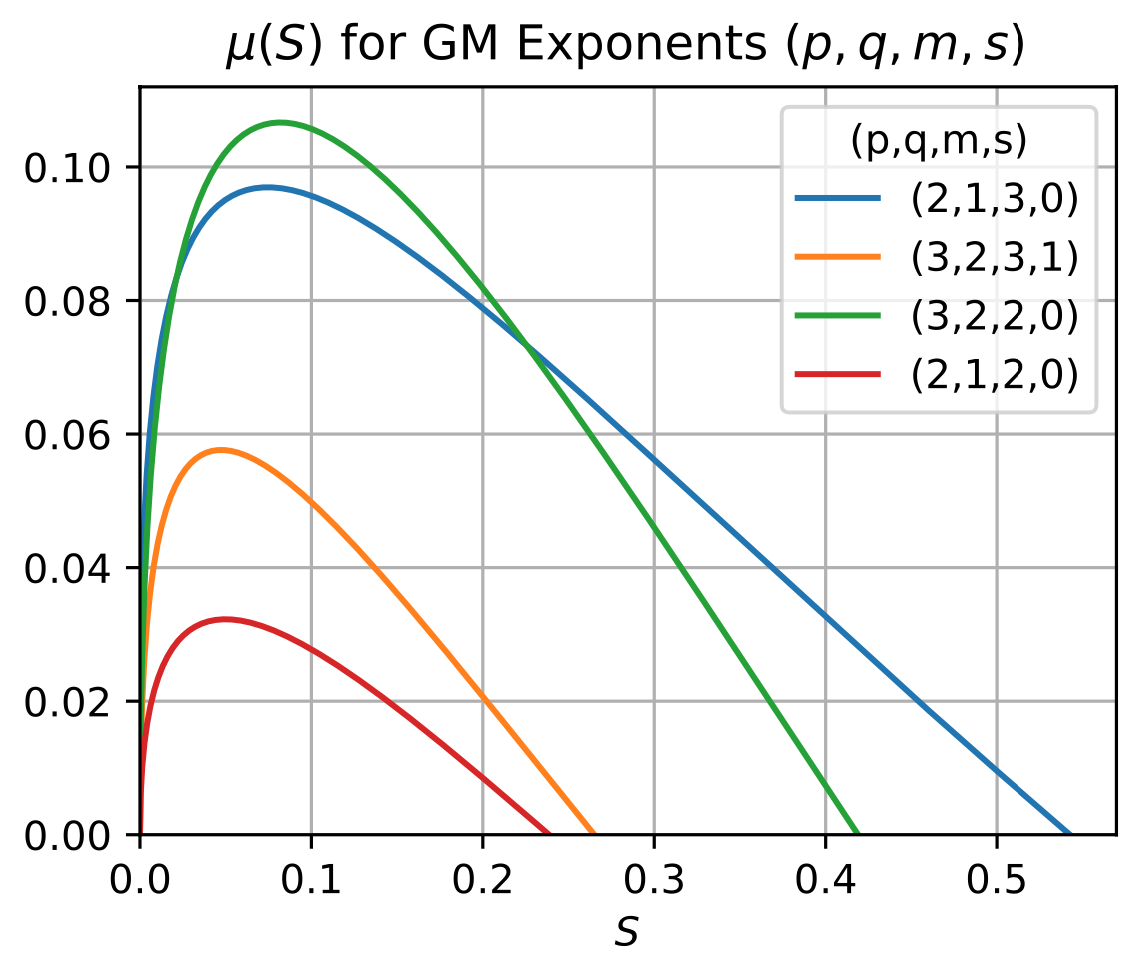
Stability of spike solutions to the fractional Gierer-Meinhardt system in a one-dimensional domain, with J. Wei and W. Yang. Numerical Mathematics: Theory, Methods and Applications (2022). (36 pages)
Boundary layer solutions in the Gierer-Meinhardt system, with inhomogeneous boundary conditions, with L. Mei and J. Wei. Physica D: Nonlinear Phenomena (2022). (16 pages)
Pattern forming systems coupling linear bulk diffusion to dynamically active membranes or cells, with S. Iyaniwura, F. Paquin-Lefebvre, and M.J. Ward. Phil. Trans. R. Soc. A. (2021). (22 pages)
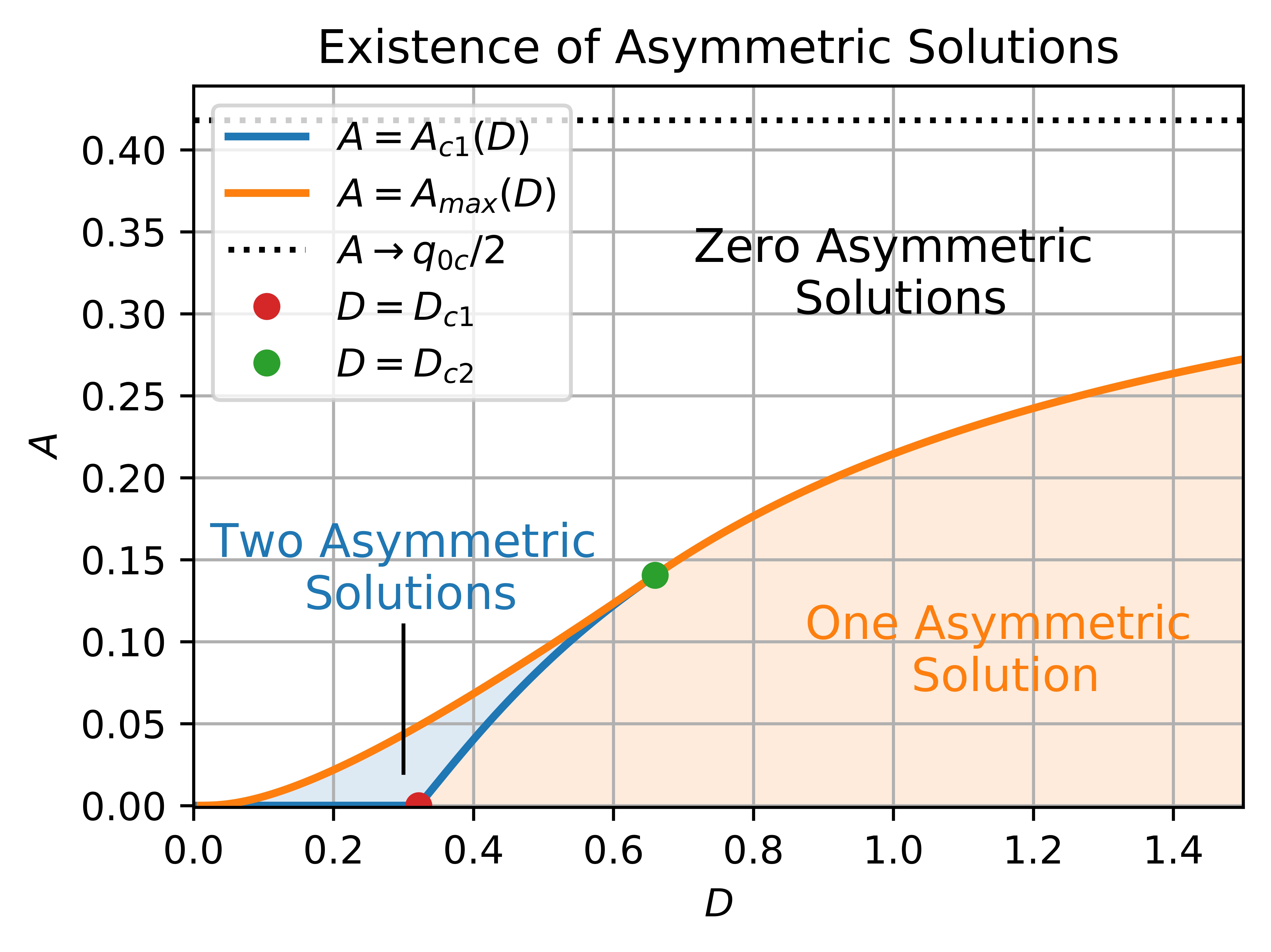
Multi-spike patterns in the Gierer-Meinhardt system, with a nonzero activator boundary flux, with J. Wei. J. Nonlinear Sci. (2021). (41 pages)
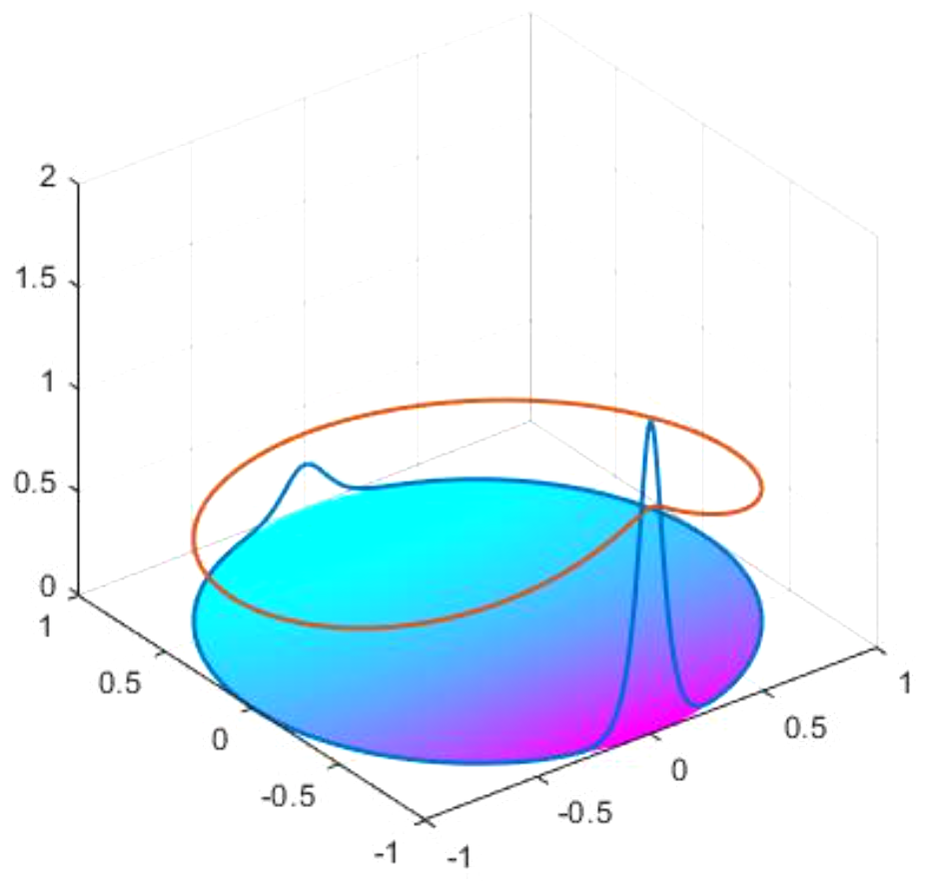
An asymptotic analysis of localized three-dimensional spot patterns for the Gierer-Meinhardt model: existence, linear stability, and slow dynamics, with M.J. Ward and J. Wei. SIAM J. Appl. Math. (2021). (29 pages)
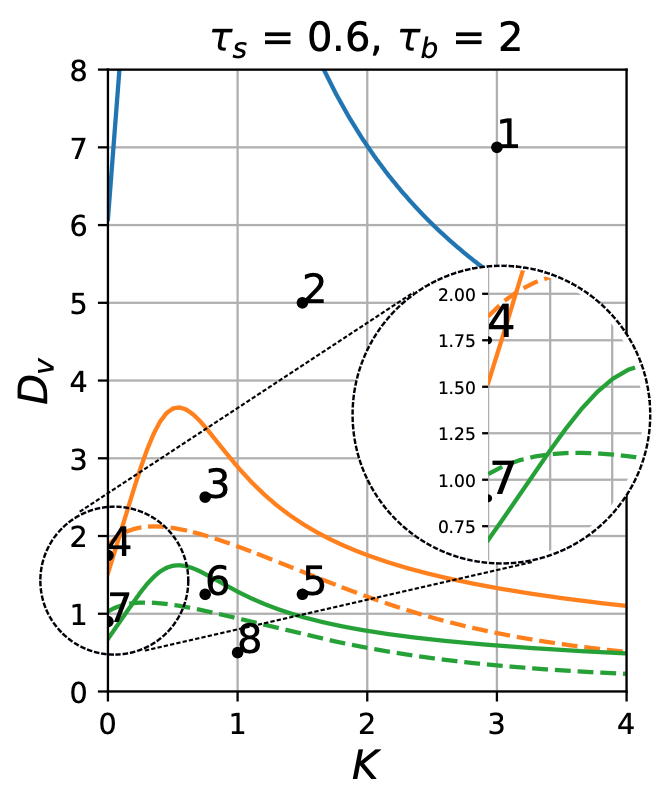
Hopf bifurcations from spike solutions for the weak coupling Gierer-Meinhardt system, with L. Mei and J. Wei. European Journal of Applied Mathematics (2021). (33 pages)
The linear stability of symmetric spike patterns for a bulk-membrane coupled Gierer-Meinhardt model, with M.J. Ward and J. Wei. SIAM J. Appl. Dyn. Syst. (2019). (40 pages)
Stable and unstable periodic spiky solutions for the Gray-Scott system and the Schnakenberg system, with L. Mei and J. Wei. J. Dyn. Diff. Eqns. (2019). (41 pages)
On isospectral deformations of an inhomogeneous string, with K. Colville and J. Szmigielski. Comm. Math. Physics 348 no. 3 (2016). (12 pages)
Asymptotic analysis of narrow escape problems in nonspherical three-dimensional domains, with A.F. Shevyakov. Phys. Rev. E. (2015). (12 pages)
The Canada Day Theorem, with H. Lundmark and J. Szmigielski. Electron. J. Combin. (2013). (16 pages)

Existence and Stability of a Boundary Layer with an Interior Spike in the Singularly Perturbed Shadow Gierer-Meinhardt System, with J. Wei (19 pages)
First Hitting Time of a One-Dimensional Levy Flight to Small Targets, with S. Lawley (21 pages)
Spike solutions to the supercritical fractional Gierer-Meinhardt system, with M. De Medeiros, J. Wei, and W. Yang. (41 pages)

An analysis of localized patterns in some novel reaction diffusion models. Ph.D. thesis supervised by M.J. Ward and J. Wei at UBC (2020).
A non-singular integral equation formulation of permeable semi-infinite hydraulic fractures driven by shear-thinning fluids. M.Sc. thesis supervised by A. Peirce and M.J. Ward at UBC (2016).