Introduction
I am interested in a variety of topics in biological and soft condensed matter physics. Computational and statistical physics ideas from soft condensed matter research offer powerful methods for gaining insights into the physics of biological processes occuring at the cellular level. During my graduate studies, I worked on problems related to biological motility. I am currently working on several problems related to chromosome organization and DNA mechanics and dynamics. Below is a summary of some of my recent endeavors.Self-organization of the cell nucleus
I am interested in the mechanics and self-organization of cell nuclei. Studying mechanics facilitates building models for nuclear morphology.
Mechanics and dynamics of DNA
I have developed a nonequilibrium theoretical model for torque and twist dynamics of DNA.
More recently, I have been working with Sumitabha Brahmachari on modeling DNA braids.
Protein-DNA binding and reaction kinetics
I have worked on a simple theoretical model for dissociation of Fis from DNA.
Kinetochore-microtubule dynamics
During metaphase of eukaryotic mitosis, chromsomes appear to oscillate about mid-cell as they are pulled back and forth by microtubules. In collaboration with Mike Lampson of the biology department, we developed a simple model to explain this behavior and other features of mitosis in eukaryotes. Recent paper in PNAS.T cell migration
The deployment of cytotoxic T cells is a crucial part of the body's adaptive immune defenses against infection. In collaboration with Chris Hunter's group in the department of pathobiology, we studied the migration of immune cells in tissue, and attempt to understand how specific biochemical signals, such as chemokines, affect migratory behavior and in turn, how migration contributes to the immune response.
We analyzed the migratory behavior of CD8+ T cells. We quantitatively characterized the migration statistics of T cells in order to understand their observed behavior in a broader biological context. Interestingly, we found that T cells migration does not conform to simple Brownian walk statistics; rather, they perform generalized Lévy walks, alternating between runs and pauses drawn from a Lévy distribution. Interestingly, this differs from our observations of T cell migration in lymph nodes. This observation raises many new questions about how T cells search for infectious targets and interact with their environment.
The video above, made by Penn's Office of Communications, explains our general results. More detailed information can be found in our paper.
Bacterial chromosome segregation
When a cell divides, it must reliably replicate its DNA and pass the replicated chromosomes and plasmids along to its daughter cell. Although this process is fundamental to all cells, the force-generating mechanisms underlying chromosome segregation are not well-understood. At a glance, the mechanism of chromosome segregation in Caulobacter crescentus is counterintuitive. Once DNA replication begins at one cell pole, a segment of the replicated chromosome (parS) is coated with the ParB protein. Meanwhile, a structure of actin-like ParA protein grows from the opposite cell pole until contacting the ParB-decorated chromosome. ParB binds to ParA and begins to disassemble it. As ParA retracts by depolymerization, it pulls the ParB-coated chromosome across the cell. No other components are known to be necessary for this process. How can ParA pull the chromosome at the very points that seem to be disintegrating?
In our paper with Ned Wingreen and Zemer Gitai at Princeton, we explain that self-diffusiophoresis is sufficient for robust chromosome pulling. This mechanism for chromosome motility relies on self-generated and self-sustaining concentration gradients. Since the ParB attached to the chromosome depolymerizes ParA, it creates a concentration gradient of ParA; since it ParB is attracted to ParA, it moves up the gradient towards higher ParA concentrations. This steady-state process pulls the DNA across the cell, as can be seen in our Brownian dynamics simulations.
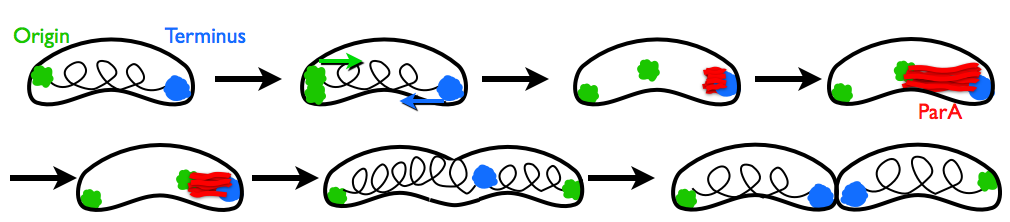
Some experimental images of this process in C. crescentus and Vibrio cholerae can be seen in papers by Shebelut et al. (2010) PNAS 107:14194 and Fogel and Waldor (2006) Genes Dev. 20:3269, respectively.
Actin-polymerization-driven motility
During actin-based motility, a cell polymerizes actin protein into a dense, branched network behind the leading edge of the cell membrane. This protein network is involved in creating membrane protrusions and assisting in cellular motility. A model system for actin-based motility is Listeria monocytogenes, which infects larger cells and hijacks their actin-polymerization machinery. In doing so, it develops a dense actin network behind its rear surface, which propels it forward. As it moves, the actin network continues to grow behind the bacterium, so that propulsion is maintained in steady-state. This process has previously been studied by Kun-Chun Lee and Andrea Liu. In their two papers, they propose that self-diffusiophoresis, relying on a bacterium-generated actin concentration gradient that drives the bacteria forward by repulsive interactions, can explain the mechanism of propulsion and force-velocity relation of actin-based motility.
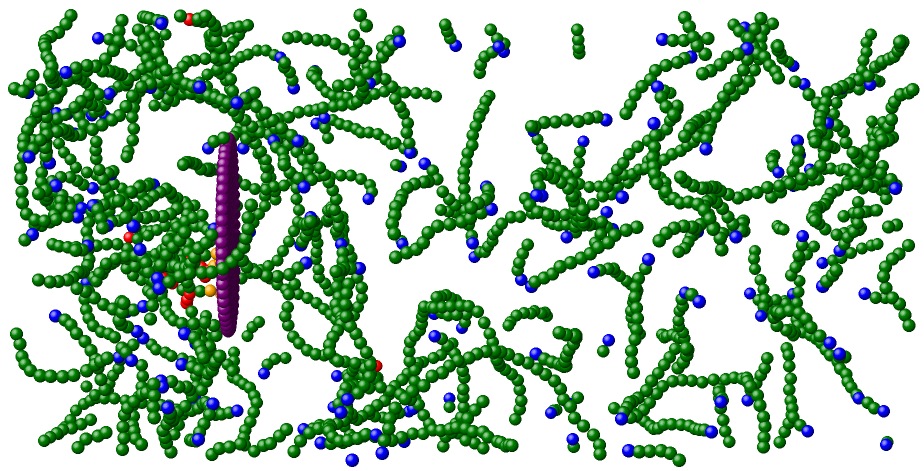
One remaining question is whether the mechanism of motility can be sustained in the presence of proteins that bind actin to the bacterial surface. Recently, we have found that cellular motility is not disrupted by the presence of local attractive interactions between the bacterium and actin, and is thus insensitive to the inclusion of proteins that bind the actin network to the bacterium. More information can be found in our paper.
Sheared granular materials
Granular systems are a rich and interesting topic of study in condensed matter physics. Working with Dave Egolf at Georgetown, I studied the dynamics of dense 2D sheared granular systems. As shown below, when granular systems are sheared, the shear stress gets distributed heterogeneously throughout the medium, thereby forming stress chains. In the image below from our MD simulations, red indicates high stress and blue indicates low stress. We have found that nonlinear dynamical quantities, such as the Lyapunov exponents and vectors, are correlated with interesting rearrangement events during shearing. Moreover, we find that these quantities are associated with time and length scales that diverge as the packing fraction is increased.
Our results were recently published in Nature Physics (as the cover article) with an accompanying commentary.

Fluid flow in cells
In collaboration with Timon Idema at Delft, I am studying how fluid flow during mitosis might affect physical processes inside the cell during mitosis.
