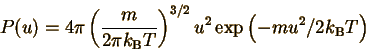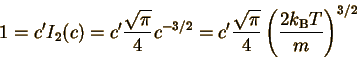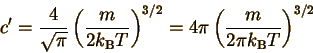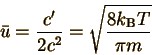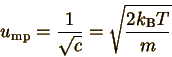Finding Average Gas Properties from the MBS DistributionThe Maxwell-Boltzmann speed (MBS) distribution tells the probability of finding a molecule with a particular speed in a gas. In this section, you will learn how to find overall properties of the gas as a whole: the average speed, the average kinetic energy, and the most probable speed. Part 1: simplifying the MBS distribution and finding normalization constant
We begin with the MBS distribution (remember that exp(x)=ex):
Let's define constants c and c' so that P(u)=c'u2 exp(-cu2) The whole point is just to make this function easier to deal with. The constant c is defined to make the exponent of P(u) correct: We can also deduce the definition of c' by comparing with the form of P(u). But we don't even have to! In the section on probability distributions, we found that a probability distribution must be normalized. Since the MBS is a continuous distribution, the normalization condition is
We can now evaluate this definite integral: (See the mathematics section below for step-by-step instructions on how to do this.)
Solving this for c' gives
This is the same constant
shown in your textbook and in the top equation on this page....BUT
WE DERIVED IT, just from knowing that all probability distributions
must be normalized!
Part 2: average speed and average kinetic energy
Once we know the probability
distribution, we have all the information we need to find average values.
The average value of a quantity is just the value in each state, weighted
by the probability of finding the system in this state. For each speed
u, the probability of finding a molecule with this speed is simply P(u).
So the average speed,
Note that the extra power of u is why this integral involves I3(c) rather than I2(c) as found in the normalization integral. Again, the mathematics section permits us to evaluate this integral:
We can also find the average
kinetic energy of molecules in the gas, by finding the weighted average
of
We can simplify this integral, and plug in for c' and c:
It is common to define 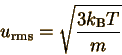 (Please note:
Part 3: most probable speed
The most probable speed is the speed u for which P(u) has a maximum. For a function to have a maximum or minimum, its first derivative must equal 0:
The expression exp(-cu2) never becomes zero, so it can be divided out, leaving 2 c'u (-cu2+1) = 0 We can see clearly that u=0 is a minimum, not a maximum, so the only possible solution is cu2=1, or
Exercises to Illustrate Average Gas Properties
The Big Picture© Andrew M. Rappe |
TheRappeGroup